代数-数学-知识点同步搜题

选择知识点

题型：

全部选择题填空题解答题

难易程度：

全部易较易中档较难难

题类筛选：

全部历年真题模拟题期末考试期中考试月考试卷单元测试其他

年份：

全部 2022 2021 2020 2019 2018 2017 更早

总题量：662选择本页全部试题

题型：填空题题类：模拟题难易度：中档
新
年份：2020

已知\(f(x)=4\sin x+3\cos x\)，\(f(x)\)向右平移\(α(0 < α < π)\)个单位后为奇函数，则\(\tan α=\)______，若方程\(f(x)-m=0\)在\([α , π]\)上恰有两个不等的根，则\(m\)的取值范围是______．

查看解析收藏纠错

+选题
题型：填空题题类：模拟题难易度：中档
新
年份：2020

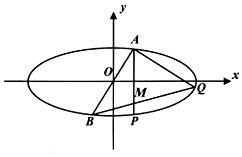如图，过原点\(O\)的直线\(AB\)交椭圆\(C： \dfrac {x^{2}}{a^{2}}+ \dfrac {y^{2}}{b^{2}}=1(a > b > 0)\)于\(A\)，\(B\)两点，过点\(A\)分别作\(x\)轴、\(AB\)的垂线\(AP.AQ\)交椭圆\(C\)于点\(P.Q\)，连接\(BQ\)交\(AP\)于一点\(M\)，若\( \overrightarrow {AM}= \dfrac {4}{5} \overrightarrow {AP}\)，则椭圆\(C\)的离心率是______．

查看解析收藏纠错

+选题
题型：填空题题类：模拟题难易度：中档
新
年份：2020

已知椭圆\(C\)：\( \dfrac {x^{2}}{4}+ \dfrac {y^{2}}{m} =1\)的右焦点为\(F(1 , 0)\)，上顶点为\(B\)，则\(B\)的坐标为______，直线\(MN\)与椭圆\(C\)交于\(M\)，\(N\)两点，且\(\triangle BMN\)的重心恰为点\(F\)，则直线\(MN\)斜率为______．

查看解析收藏纠错

+选题
题型：填空题题类：模拟题难易度：中档
新
年份：2020

已知点\(P\)是椭圆\( \dfrac {x^{2}}{9}+ \dfrac {y^{2}}{5}=1\)上的动点，\(F _{1}\)、\(F _{2}\)分别为椭圆的左、右焦点，\(O\)为坐标原点，若\(M\)是\(∠F _{1} PF _{2}\)的角平分线上的一点，且\(MF _{1} ⊥MP\)，则\(OM\)的取值范围是______．

查看解析收藏纠错

+选题
题型：填空题题类：模拟题难易度：中档
新
年份：2020

在\(\triangle ABC\)中，角\(A\)，\(B\)，\(C\)所对的边分别是\(a\)，\(b\)，\(c\)，\(2ab\sin A+(ac-6)\sin 2B=2b ^{2} \sin A\cos C\)，则\(ac=\)______，若\(\triangle ABC\)的面积\(S=1\)，则\(\cos ( \dfrac {B}{2}- \dfrac {π}{4} )═\)______．

查看解析收藏纠错

+选题
题型：填空题题类：模拟题难易度：中档
新
年份：2020

设点\(O\)为\(\triangle ABC\)的外心，且\(A= \dfrac {π}{3}\)，若\( \overrightarrow {AO} =α \overrightarrow {AB} + β \overrightarrow {AC} (α , β∈R)\)，则\(α+β\)的最大值为______．

查看解析收藏纠错

+选题
题型：填空题题类：模拟题难易度：中档
新
年份：2020

若实数\(a\)、\(b\)、\(c\)满足\( \dfrac {1}{a} + \dfrac {1}{b} ═ \dfrac {2}{c}\)，则\(a\)，\(b\)，\(c\)是调和的．设含有三个元素的集合\(P\)是集合\(M=\{x||x|\leqslant 2020 , x∈Z\}\)的子集，当集合\(P\)中的元素\(a\)、\(b\)、\(c\)既是等差的又是调和的时，称集合\(P\)为“好集”\(.\)则三元子集中“好集”的概率是______．

查看解析收藏纠错

+选题
题型：填空题题类：模拟题难易度：中档
新
年份：2020

在三棱锥\(S-ABC\)中，\(AB=6\)，\(BC=8\)，\(AC=10\)，二面角\(S-AB-C\)、\(S-AC-B\)、\(S-BC-A\)的大小均为\( \dfrac {π}{4}\)，设三棱锥\(S-ABC\)的外接球球心为\(O\)，直线\(SO\)交平面\(ABC\)于点\(M\)，则三棱锥\(S-ABC\)的内切球半径为______，\( \dfrac {SO}{OM} =\)______．

查看解析收藏纠错

+选题
题型：填空题题类：模拟题难易度：中档
新
年份：2020

已知正四棱椎\(P-ABCD\)中，\(\triangle PAC\)是边长为\(3\)的等边三角形，点\(M\)是\(\triangle PAC\)的重心，过点\(M\)作与平面\(PAC\)垂直的平面\(α\)，平面\(α\)与截面\(PAC\)交线段的长度为\(2\)，则平面\(α\)与正四棱椎\(P-ABCD\)表面交线所围成的封闭图形的面积可能为______\(.(\)请将可能的结果序号横线上\()\)
①\(2\)；②\(2 \sqrt {2}\)；③\(3\)；④\(2 \sqrt {3}\)．

查看解析收藏纠错

+选题
题型：填空题题类：模拟题难易度：中档
新
年份：2020

已知等比数列\(\{a _{n} \}\)的公比为\(q\)，且\(0 < a _{1} < 1\)，\(a _{2020} =1\)，则\(q\)的取值范围为______；能使不等式\((a_{1}- \dfrac {1}{a_{1}})+(a_{2}- \dfrac {1}{a_{2}})+…+(a_{m}- \dfrac {1}{a_{m}})\leqslant 0\)成立的最大正整数\(m=\)______．

查看解析收藏纠错

+选题

高中

选择知识点

服务介绍

帮助中心