代数-数学-知识点同步搜题

选择知识点

题型：

全部选择题填空题解答题

难易程度：

全部易较易中档较难难

题类筛选：

全部历年真题模拟题期末考试期中考试月考试卷单元测试其他

年份：

全部 2025 2024 2023 2022 2021 2020 更早

总题量：2186选择本页全部试题

题型：解答题题类：月考试卷难易度：难
新
年份：2020

已知函数\(y=x+ \dfrac {a}{x}\)有如下性质：如果常数\(a > 0\)，那么该函数在\((0 , \sqrt {a} ]\)上是减函数，在\([ \sqrt {a} , +∞)\)上是增函数．
\((\)Ⅰ\()\)如果函数\(y=x+ \dfrac {2^{b}}{x} (x > 0)\)的值域为\([6 , +∞)\)，求\(b\)的值；
\((\)Ⅱ\()\)研究函数\(y=x ^{2} + \dfrac {c}{x^{2}} (\)常数\(c > 0)\)在定义域内的单调性，并说明理由；
\((\)Ⅲ\()\)对函数\(y=x+ \dfrac {a}{x}\)和\(y=x ^{2} + \dfrac {a}{x^{2}} (\)常数\(a > 0)\)作出推广，使它们都是你所推广的函数的特例．研究推广后的函数的单调性\((\)只须写出结论，不必证明\()\)，并求函数\(F(x)=(x ^{2} + \dfrac {1}{x} ) ^{n} +( \dfrac {1}{x^{2}}+x ) ^{n} (n\)是正整数\()\)在区间\([ \dfrac {1}{2} , 2]\)上的最大值和最小值\((\)可利用你的研究结论\()\)．

查看解析收藏纠错

+选题
题型：选择题题类：月考试卷难易度：难
新测
年份：2020

设函数\(f(x)\text{=}\text{xsinx}\text{+}\text{cosx}\text{-}\dfrac{x^{2}}{4}\)，则下列是函数\(f(x)\)极小值点的是\((\) \()\)

A.\(\text{-}\dfrac{4\pi}{3}\) B.\(\text{-}\dfrac{\pi}{3}\) C.\(\dfrac{\pi}{3}\) D.\(\dfrac{5\pi}{3}\)

查看解析收藏纠错

+选题
题型：填空题题类：月考试卷难易度：难
新
年份：2020

已知函数\(y=f(x)+x\)是偶函数，且\(f(2)=1\)，则\(f(-2)=\) ______ ．

查看解析收藏纠错

+选题
题型：解答题题类：月考试卷难易度：难
新
年份：2020

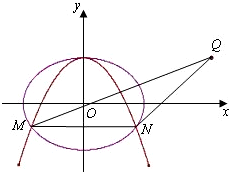已知抛物线\(C _{1}\)：\(x ^{2} +by=b ^{2}\)经过椭圆\(C _{2}\)：\( \dfrac {x^{2}}{a^{2}} + \dfrac {y^{2}}{b^{2}} =1(a > b > 0)\)的两个焦点．
\((1)\)求椭圆\(C _{2}\)的离心率；
\((2)\)设\(Q(3 , b)\)，又\(M\)，\(N\)为\(C _{1}\)与\(C _{2}\)不在\(y\)轴上的两个交点，若\(\triangle QMN\)的重心在抛物线\(C _{1}\)上，求\(C _{1}\)和\(C _{2}\)的方程．

查看解析收藏纠错

+选题
题型：选择题题类：月考试卷难易度：难
新测
年份：2020

下列说法正确的个数有\((\:\:\:\:)\)
①用\(R ^{2} =1-\)”\( \dfrac { \sum\limits_{i=1}^{n}(y_{i}- \overset{\land }{y_{i}})^{2}}{ \sum\limits_{i=1}^{n}(y_{i}- \overline {y})^{2}}\)刻画回归效果，当\(R ^{2}\)越大时，模型的拟合效果越差；反之，则越好；
②命题“\(∃x∈R\)，\(x ^{2} +x-1 < 0\)”的否定是“\(∀x∈R\)，\(x ^{2} +x-1\geqslant 0\)”；
③若回归直线的斜率估计值是\(2.25\)，样本点的中心为\((4 , 5)\)，则回归直线方程是\( \overset{\land }{y} =2.25x-4\)；
④综合法证明数学问题是“由因索果”，分析法证明数学问题是“执果索因”．

A.\(1\)个 B.\(2\)个 C.\(3\)个 D.\(4\)个

查看解析收藏纠错

+选题
题型：解答题题类：月考试卷难易度：难
新
年份：2020

正项等差数列\(\{a _{n} \}\)中，已知\(a _{1} +a _{2} +a _{3} =15\)，且\(a _{1} +2\)，\(a _{2} +5\)，\(a _{3} +13\)构成等比数列\(\{b _{n} \}\)的前三项．
\((\)Ⅰ\()\)求数列\(\{a _{n} \}\)，\(\{b _{n} \}\)的通项公式；
\((\)Ⅱ\()\)求数列\(\{a _{n} \boldsymbol{⋅}b _{n} \}\)的前\(n\)项和\(T _{n}\)．

查看解析收藏纠错

+选题
题型：解答题题类：月考试卷难易度：难
新
年份：2020

已知\(S _{n} =\{A|A=(a _{1} , a _{2} , a _{3} , …a _{n} )\}\)，\(a _{i} =\{0\)或\(1\}\)，\(i=1\)，\(2\)，\(...\)，\(n(n\geqslant 2)\)，对于\(U\)，\(V∈S _{n}\)，\(d(U , V)\)表示\(U\)和\(V\)中相对应的元素不同的个数．
\((\)Ⅰ\()\)令\(U=(0 , 0 , 0 , 0 , 0)\)，存在\(m\)个\(V∈S _{5}\)，使得\(d(U , V)=2\)，写出\(m\)的值；
\((\)Ⅱ\()\)令\(W=(0,0,...,0)(n个0)\)，\(U\)，\(V∈S _{n}\)，求证：\(d(U , W)+d(V , W)\geqslant d(U , V)\)；
\((\)Ⅲ\()\)令\(U=(a _{1} , a _{2} , a _{3} , … , a _{n} )\)，若\(V∈S _{n}\)，求所有\(d(U , V)\)之和．

查看解析收藏纠错

+选题
题型：填空题题类：月考试卷难易度：难
新
年份：2020

\(\triangle ABC\)中，角\(A\)、\(B\)、\(C\)所对的边\(a\)，\(b\)，\(c\)成等差数列，且最大角是最小角的\(2\)倍，则 \(\cos A+\cos C=\)______．

查看解析收藏纠错

+选题
题型：解答题题类：月考试卷难易度：难
新
年份：2020

已知数列\(\{a _{n} \}\)满足\(a _{n+2} +a _{n} =2a _{n+1} (n∈N ^{*} )\)，数列\(\{b _{n} \}\)满足\(\dfrac{{{b}_{n+1}}}{{{b}_{n}}}={{a}_{n+1}}-{{a}_{n}} (n∈N ^{*} )\)，且\(a _{1} =b _{1}\)，\(a _{3} =5\)，\(a _{5} +a _{7} =22\)．
\((1)\)求\(a _{n}\)及\(b _{n}\)；
\((2)\)令\(c _{n} =a _{n} b _{n}\)，\(n∈N ^{*}\)，求数列\(\{c _{n} \}\)的前\(n\)项和\(S _{n}\)．

查看解析收藏纠错

+选题
题型：解答题题类：月考试卷难易度：难
新
年份：2020

如图，设\(A\)是由\(n×n\)个实数组成的\(n\)行\(n\)列的数表，其中\(a _{ij} (i , j=1 , 2 , 3 , … , )n\)表示位于第\(i\)行第\(j\)列的实数，且\(a _{ij} ∈\{1 , -1\}.\)记\(S(n , n)\)为所有这样的数表构成的集合．对于\(A∈(n , n)\)，记\(r _{i} (A)\)为\(A\)的第\(i\)行各数之积，\(c _{j} (A)\)为\(A\)的第\(j\)列各数之积．令\(I(A)= \sum\limits_{i=1}^{n}r_{i}(A)+ \sum\limits_{j=1}^{n}C_{j}(A)\)．

\(a _{11}\) \(a _{12}\) \(…\) \(a _{1n}\)

\(a _{21}\) \(a _{22}\) \(…\) \(a _{2n}\)

\(…\) \(…\) \(…\) \(…\)

\(a _{n1}\) \(a _{n2}\) \(…\) \(a _{nn}\)

\((\)Ⅰ\()\)请写出一个\(A∈S(4 , 4)\)，使得\(l(A)=0\)；
\((\)Ⅱ\()\)是否存在\(A∈S(9 , 9)\)，使得\(l(A)=0\)？说明理由；
\((\)Ⅲ\()\)给定正整数\(n\)，对于所有的\(A∈S(n , n)\)，求\(l(A)\)的取值集合．

查看解析收藏纠错

+选题

高中

选择知识点

服务介绍

帮助中心

\(a _{11}\)	\(a _{12}\)	\(…\)	\(a _{1n}\)
\(a _{21}\)	\(a _{22}\)	\(…\)	\(a _{2n}\)
\(…\)	\(…\)	\(…\)	\(…\)
\(a _{n1}\)	\(a _{n2}\)	\(…\)	\(a _{nn}\)