代数-数学-知识点同步搜题

选择知识点

题型：

全部选择题填空题解答题

难易程度：

全部易较易中档较难难

题类筛选：

全部历年真题模拟题期末考试期中考试月考试卷单元测试其他

年份：

全部 2022 2021 2020 2019 2018 2017 更早

总题量：2158选择本页全部试题

题型：选择题题类：其他难易度：较易
新测
年份：2020

如图是一个空间几何体的正视图、侧视图和俯视图，则该几何体的形状是\((\:\:\:\:)\)

A.三棱锥 B.四棱锥 C.三棱柱 D.四棱柱

查看解析收藏纠错

+选题
题型：选择题题类：其他难易度：较易
新测
年份：2020

已知\(\triangle ABC\)的三个内角\(A\)，\(B\)，\(C\)所对的三条边为\(a\)，\(b\)，\(c\)，若\(A\)：\(B\)：\(C=1\)：\(1\)：\(4\)，则\(a\)：\(b\)：\(c= (\:\:\:\:)\)

A.\(1\)：\(1\)：\(4\) B.\(1\)：\(1\)：\(2\) C.\(1\)：\(1\)：\(3\) D.\(1\)：\(1\)：\( \sqrt {3}\)

查看解析收藏纠错

+选题
题型：选择题题类：其他难易度：较易
新测
年份：2020

设\(m\)、\(n\)是两条不同的直线，\(α\)是平面，\(m\)、\(n\)不在\(α\)内，下列结论中错误的是\((\:\:\:\:)\)

A.\(m⊥α\)，\(n/\!/α\)，则\(m⊥n\) B.\(m⊥α\)，\(n⊥α\)，则\(m/\!/n\) C.\(m⊥α\)，\(m⊥n\)，则\(n/\!/α\) D.\(m⊥n\)，\(n/\!/α\)，则\(m⊥α\)

查看解析收藏纠错

+选题
题型：选择题题类：其他难易度：较易
新测
年份：2020

设实数\(x\)，\(y\)满足约束条件\( \begin{cases} x-y\leqslant 0 \\ x+y\geqslant 0 \\ y\leqslant a\end{cases}\)，若\(z=x+2y\)的最大值为\(12\)，则\(a\)的值是\((\:\:\:\:)\)

A.\(1\) B.\(5\) C.\(2\) D.\(4\)

查看解析收藏纠错

+选题
题型：解答题题类：其他难易度：较易
新
年份：2020

已知函数\(f(x)=2\sin ωx\boldsymbol{⋅}\cos ωx(ω > 0)\)的最小正周期为\(π\)．
\((\)Ⅰ\()\)求\(ω\)的值；
\((\)Ⅱ\()\)求\(f(x)\)的单调递增区间；
\((\)Ⅲ\()\)若\(f( \dfrac {π}{4}+α)= \dfrac {2}{3}\)，\(( 0 < α < \dfrac {π}{2} )\)，求\(\sin 2α\)的值．

查看解析收藏纠错

+选题
题型：选择题题类：其他难易度：较易
新测
年份：2020

如图是某学校抽取的学生体重的频率分布直方图，已知图中从左到右的前\(3\)个小组的频率满足：第一小组与第三小组的频率和是第二小组频率的\(2\)倍，第二小组的频数为\(15\)，则抽取的学生人数为\((\:\:\:\:)\)

A.\(30\) B.\(45\) C.\(60\) D.\(120\)

查看解析收藏纠错

+选题
题型：填空题题类：其他难易度：较易
新
年份：2020

先后抛掷三枚均匀的硬币，至少出现一次正面的概率是______．

查看解析收藏纠错

+选题
题型：解答题题类：其他难易度：较易
新
年份：2020

如图，在正方体\(ABCD-EFGH\)中，
\((\)Ⅰ\()\)求证：平面\(BEG/\!/\)平面\(ACH\)；
\((\)Ⅱ\()\)求证：\(DF⊥\)平面\(BEG\)．

查看解析收藏纠错

+选题
题型：解答题题类：其他难易度：较易
新
年份：2020

已知函数\(f(x)=x ^{2} -2ax+2a ^{2} +2\)．
\((\)Ⅰ\()\)若\(a=1\)，求函数\(f(x)\)的单调区间；
\((\)Ⅱ\()\)求函数\(f(x)\)在区间\([- \dfrac {3}{2}, \dfrac {3}{2}]\)的最小值；
\((\)Ⅲ\()\)关于\(x\)的方程\(f(x)=2a ^{2}\)有解，求实数\(a\)的取值范围．

查看解析收藏纠错

+选题
题型：解答题题类：其他难易度：较易
新
年份：2020

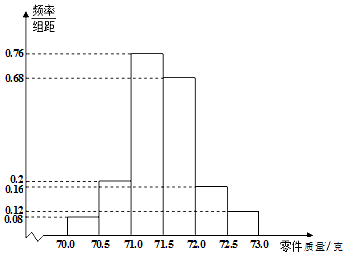
\(3\)月底，我国新冠肺炎疫情得到有效防控，但海外确诊病例却持续暴增，防疫物资供不应求．某医疗器械厂开足马力，日夜生产防疫所需物品．质量检验员为了检测生产线上零件的质量情况，从生产线上随机抽取了\(50\)个零件进行测量，根据所测量的零件质量\((\)单位：克\()\)，得到如图的频率分布直方图：
\((1)\)根据频率分布直方图，求这\(50\)个零件质量的中位数\((\)结果精确到\(0.01)\)；
\((2)\)若从这\(50\)个零件中质量位于\([70.5 , 72.5)\)之外的零件中随机抽取\(2\)个，求这两个零件中恰好有\(1\)个是质量在\([72.5 , 73]\)上的概率
\((3)\)以各组数据的中间数值代表这组数据的平均水平，以频率代表概率，已知这批零件有\(10000\)个，某采购商提出两种收购方案：
A.所有零件均以\(50\)元\(/\)百克收购；
B.质量位于\([71.0 , 72)\)的零件以\(40\)元\(/\)个收购，其他零件以\(30\)元\(/\)个收购．
请你通过计算为该厂选择收益最好的方案．

查看解析收藏纠错

+选题

高中

选择知识点

服务介绍

帮助中心