题型：选择题 题类：模拟题 难易度：难
测年份：2018
已知抛物线\(C:{{y}^{2}}=2px(p > 0)\)的焦点为\(F\)，点\(M\left( {{x}_{0}},2\sqrt{2} \right)({{x}_{0}} > \dfrac{p}{2})\)是抛物线\(C\)上一点，圆\(M\)与线段\(MF\)相交于点\(A\)，且被直线\(x=\dfrac{p}{2}\)截得的弦长为\(\sqrt{3}\left| MA \right|.\)若\(\dfrac{\left| MA \right|}{\left| AF \right|}=2\)，则\(\left| AF \right|\)等于( )
题型：选择题 题类：模拟题 难易度：难
测年份：2018
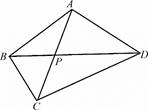
如图，平面四边形\(ABCD\)中，\(AC\)与\(BD\)交于点\(P\)，若\(3\overrightarrow{AP}+\overrightarrow{BD}=3\overrightarrow{BC}\)，\(AB=AD=\sqrt{3}BC\)，\(\angle CAD+\angle ACB=\dfrac{5}{6}\pi \)，则\(\dfrac{CD}{AB}=(\) \()\)
时，称△ABC为“和谐三角形”，则“和谐三角形”有（ ） 
绕y轴旋转一周得到的几何体叫做椭球体，记为G1，几何体G2的三视图如图所示．根据祖暅原理通过考察G2可以得到G1的体积，则G1的体积为（ ）
