代数-数学-知识点同步搜题

选择知识点

题型：

全部选择题填空题解答题

难易程度：

全部易较易中档较难难

题类筛选：

全部历年真题模拟题期末考试期中考试月考试卷单元测试其他

年份：

全部 2022 2021 2020 2019 2018 2017 更早

总题量：5154选择本页全部试题

题型：解答题题类：月考试卷难易度：较易
新
年份：2020

设函数\(f(x)=\cos x\boldsymbol{⋅}\sin (x+ \dfrac {π}{3} )- \sqrt {3} \cos ^{2} x+ \dfrac { \sqrt {3}}{4}\)，\(x∈R\)．
\((1)\)求\(f(x)\)的最小正周期和对称中心；
\((2)\)若函数\(f(x)\)的图象向左平移\( \dfrac {π}{4}\)个单位得到函数\(g(x)\)的图象，求函数\(g(x)\)在区间\([- \dfrac {π}{6}, \dfrac {π}{4}]\)上的值域．

查看解析收藏纠错

+选题
题型：解答题题类：月考试卷难易度：较易
新
年份：2020

\(\triangle ABC\)的内角\(A\)，\(B\)，\(C\)的对边分别为\(a\)，\(b\)，\(c\)，若\(2\sin ^{2} \dfrac {A-B}{2} +2\cos ^{2} \dfrac {A+B}{2} +2\cos A\cos B=1\)．
\((1)\)求角\(C\)的大小；
\((2)\)若\(c=4\)，\(| \overrightarrow {CA} + \overrightarrow {CB} |= \sqrt {38} .\)求\(\triangle ABC\)的周长．

查看解析收藏纠错

+选题
题型：解答题题类：月考试卷难易度：较易
新
年份：2020

在\(\triangle ABC\)中，内角\(A\)，\(B\)，\(C\)所对的边长分别为\(a\)，\(b\)，\(c\)，且满足\( \dfrac {2\tan B}{\tan A+\tan B}= \dfrac {b}{c}\)．
\((\)Ⅰ\()\)求角\(A\)；
\((\)Ⅱ\()\)若\(a= \sqrt {13}\)，\(b=3\)，求\(\triangle ABC\)的面积．

查看解析收藏纠错

+选题
题型：解答题题类：月考试卷难易度：较易
新
年份：2020

已知函数\(f(x)=\cos (ωx+ \dfrac {π}{6} )(0 < ω < 3)\)的零点为\(x= \dfrac {π}{6}\)．
\((1)\)求函数\(f(x)\)的最小正周期；
\((2)\)求函数\(f(x)\)在\([-π , 0]\)上的单调递减区间．

查看解析收藏纠错

+选题
题型：解答题题类：月考试卷难易度：较易
新
年份：2020

在\(\triangle ABC\)中，内角\(A\)，\(B\)，\(C\)的对边分别为\(a\)，\(b\)，\(c\)，且满足\( \sqrt {3} (b\cos C-a)=c\sin B\)，\(b=2 \sqrt {3}\)．
\((1)\)求\(B\)；
\((2)\)若\(a+c=4\)，求\(\triangle ABC\)的面积．

查看解析收藏纠错

+选题
题型：解答题题类：月考试卷难易度：较易
新
年份：2020

已知数列\(\{a _{n} \}\)的前\(n\)项和为\(S _{n}\)，\(a _{1} =1\)，\((n-1)S _{n} =nS _{n-1} +(n-1)n(n∈N _{+} , n\geqslant 2)\)．
\((1)\)求证：数列\(\{ \dfrac {S_{n}}{n}\}\)为等差数列；
\((2)\)记数列\(\{ \dfrac {1}{a_{n}a_{n+1}}\}\)的前\(n\)项和为\(T _{n}\)，求\(T _{n}\)．

查看解析收藏纠错

+选题
题型：解答题题类：月考试卷难易度：较易
新
年份：2020

已知函数\(f(x)=2\sin (ωx+φ)(ω > 0,|φ| < \dfrac {π}{2})\)的最小正周期为\(π\)，且图象经过点\((0 , 1)\)，求函数\(f(x)\)在区间\([ - \dfrac {π}{3} , 0]\)上的值域．

查看解析收藏纠错

+选题
题型：解答题题类：期中考试难易度：较易
新
年份：2020

等差数列\(\{a _{n} \}\)满足\(a _{1} +a _{2} =10\)，\(a _{4} -a _{3} =2\)．
\((1)\)求\(\{a _{n} \}\)的通项公式；
\((2)\)设等比数列\(\{b _{n} \}\)满足\(b _{2} =a _{3}\)，\(b _{3} =a _{7}\)，求数列\(\{b _{n} \}\)的前\(n\)项和．

查看解析收藏纠错

+选题
题型：解答题题类：月考试卷难易度：较易
新
年份：2020

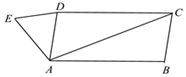为建设美丽新农村，某村对本村布局重新进行了规划，其平面规划图如图所示，其中平行四边形\(ABCD\)区域为生活区，\(AC\)为横穿村庄的一条道路，\(\triangle ADE\)区域为休闲公园，\(BC=200m\)，\(∠ACB=∠AED=60°\)，\(\triangle ABC\)的外接圆直径为\( \dfrac {200 \sqrt {57}}{3}m\)．
\((\)Ⅰ\()\)求道路\(AC\)的长；
\((\)Ⅱ\()\)该村准备沿休闲公园的边界修建栅栏，以防村中的家畜破坏公园中的绿化，试求栅栏总长的最大值．

查看解析收藏纠错

+选题
题型：解答题题类：期中考试难易度：较易
新
年份：2020

已知函数\(f(x)=\ln (x ^{-1} +a)\)．
\((1)\)设\(f ^{-1} (x)\)是\(f(x)\)的反函数，当\(a=1\)时，解不等式\(f ^{-1} (x) > 0\)；
\((2)\)若关于\(x\)的方程\(f(x)+1n(x ^{2} )=0\)的解集中恰好有一个元素，求实数\(a\)的值；
\((3)\)设\(a > 0\)，若对任意\(t∈[ \dfrac {1}{2} , 1]\)，函数\(f(x)\)在区间\([t , t+1]\)上的最大值与最小值的差不超过\(1n2\)，求\(a\)的取值范围．

查看解析收藏纠错

+选题

高中

选择知识点

服务介绍

帮助中心