代数-数学-知识点同步搜题

选择知识点

题型：

全部选择题填空题解答题

难易程度：

全部易较易中档较难难

题类筛选：

全部历年真题模拟题期末考试期中考试月考试卷单元测试其他

年份：

全部 2022 2021 2020 2019 2018 2017 更早

总题量：987选择本页全部试题

题型：解答题题类：期末考试难易度：难
新
年份：2025

(本题8分)在△ABC中,角A、B、C所对的边分别为\( a\),b,c,已知\( \mathrm{c}\mathrm{o}\mathrm{s}2C=-\frac{1}{4}.\)
(1)求sinC的值;
(2)当\( a\)=2，2sinA=sinC时，求b及c的长

查看解析收藏纠错

+选题
题型：解答题题类：期末考试难易度：难
新
年份：2025

(本题8分)如图所示四棱锥S-ABCD中,底面ABCD为正方形,SD⊥平面ABCD,SD=DC=1,E,F分别为SD,BD的中点,
(1)求证:CF⊥平面DEF.
(2)求EF与BC所成角的正弦值.

查看解析收藏纠错

+选题
题型：解答题题类：期末考试难易度：难
新
年份：2025

(本题9分)设椭圆\( \frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1\left(a\right.⟩b>0)\)的左、右焦点分别为\( F₁，F₂\),点P(a,b)满足\( |PF₂|=|F₁F₂|.\)
(1)求椭圆的离心率e：
(2)设直线PF₂与椭圆相交于A，B两点，若直线PF₂与圆(\( {\left(x+1\right)}^{2}+{\left(y-\sqrt{3}\right)}^{2}=16\)相交于M，N两点，且\( \left|MN\right|=\frac{5}{8}\left|AB\right|,\)求椭圆的方程

查看解析收藏纠错

+选题
题型：解答题题类：期末考试难易度：难
新
年份：2022

已知圆\( C:{x}^{2}＋{y}^{2}-4x-6y＋9=0,直线l：\)tx\( －\)y＋1=0
(1)若直线l经过圆C的圆心\( ,\)求t的值;
(2)若直线l与圆C相交\( \mathrm{M}\mathrm{、}\mathrm{N}\mathrm{两}\mathrm{点},且\overrightarrow{OM}\cdot \overrightarrow{ON}=9\)求实数t的值

查看解析收藏纠错

+选题
题型：解答题题类：期末考试难易度：难
新
年份：2022

求函数\( y=11-8cosx-2si{n}^{2}x\)的最大值与最小值\( ,\)并写出使函数y取最值时的x的集合.

查看解析收藏纠错

+选题
题型：解答题题类：期末考试难易度：难
新
年份：2022

某工厂三年的生产计划是从第二年起,每一年比上一年增加的产值相同,三年的总产值为300万元,如果三年分别比原计划的产值多10万元、10万元、11万元,那么每一年比上一年的产值增长的百分率相同.求原计划各年的产值.

查看解析收藏纠错

+选题
题型：解答题题类：期末考试难易度：难
新
年份：2022

已知斜率为1的直线l过椭圆\( \frac{{x}^{2}}{3}＋\frac{{y}^{2}}{2}=1\)的右焦点F₂\( ,\)并交椭圆于A\( ,\)B两点\( ,\)求:
(1)弦长|AB|;
(2)△AF₁B的面积(F₁是左焦点).

查看解析收藏纠错

+选题
题型：解答题题类：期末考试难易度：难
新
年份：2022

已知椭圆\( \frac{{x}^{2}}{4}＋{y}^{2}=1,点P(1,\frac{1}{2})\)直线l过点P与椭圆交于M\( ,\)N两点\( ,\)若点P平分线段MN\( ,\)求直线l的方程.

查看解析收藏纠错

+选题
题型：解答题题类：期末考试难易度：难
新
年份：2022

求椭圆\( \frac{{x}^{2}}{9}＋\frac{{y}^{2}}{16}=1\)上的点到直线x＋y\( －\)7=0的最短距离

查看解析收藏纠错

+选题
题型：解答题题类：期末考试难易度：难
新
年份：2022

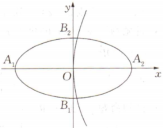
已知抛物线的顶点在坐标.原点\( ,\)椭圆\( \frac{{x}^{2}}{4}＋{y}^{2}=1\)的顶点分别为\( {A}_{1},{A}_{2},{B}_{1},{B}_{2},\)其中点A₂为抛物线的焦点\( ,\)如图所示
(1)求抛物线的标准方程;
(2)若过点A₁的直线l与抛物线交于M\( ,\)N两点\( ,\)且\( (\overrightarrow{OM}＋\overrightarrow{ON})//|\overrightarrow{{B}_{1}{A}_{2}},\)求直线l的方程.

查看解析收藏纠错

+选题

高中

选择知识点

服务介绍

帮助中心