代数-数学-知识点同步搜题

选择知识点

题型：

全部选择题填空题解答题

难易程度：

全部易较易中档较难难

题类筛选：

全部历年真题模拟题期末考试期中考试月考试卷单元测试其他

年份：

全部 2022 2021 2020 2019 2018 2017 更早

总题量：46选择本页全部试题

题型：解答题题类：期末考试难易度：难
新
年份：2020

一农妇原有\(a _{0} ∈N*\)个鸡蛋，现分\(9\)次售卖鸡蛋，设每次卖出后剩下的鸡蛋个数依次为\(a _{1}\)，\(a _{2}\)，\(…\)，\(a _{9}\)个．
\((\)Ⅰ\()\)如果农妇第一次卖去全部鸡蛋的一半又半个，第二次卖去剩下的一半又半个，第三次又卖去剩下的一半又半个，\(…\)，第九次仍然卖去剩下的一半又半个，而且这次恰好全部卖完，求\(a _{9}\)，\(a _{8}\)，\(a _{7}\)，给出数列\(\{a _{n} \}\)的递公式并据此求出\(a _{0}\)；
\((\)Ⅱ\()\)鸡蛋无法分割出售，如果农妇原有鸡蛋\(a _{0} =511\)个，是否存在\(p\)，\(q∈N*\)，\((p > 2)\)，使得农妇按如下方式卖鸡蛋：第一次卖去全部的\( \dfrac {1}{p}\)又\( \dfrac {1}{q}\)个，第二次卖去剩下的\( \dfrac {1}{p}\)又\( \dfrac {1}{q}\)个，第三次又卖去剩下的\( \dfrac {1}{p}\)又\( \dfrac {1}{q}\)个，\(…\)，第九次仍然卖去剩下的\( \dfrac {1}{p}\)又\( \dfrac {1}{q}\)个，而且这次恰好全部卖完？如果存在，求出可能的\(p\)，\(q\)的值，如果不存在，请说明理由．

查看解析收藏纠错

+选题
题型：解答题题类：期末考试难易度：难
新
年份：2020

已知集合\(A\)为非空数集，定义\(A ^{+} =\{x|x=a+b , a , b∈A\}\)，\(A ^{-} =\{x|x=|a-b| , a , b∈A\}\)．
\((1)\)若集合\(A=\{-1 , 1\}\)，直接写出集合\(A ^{+}\)及\(A ^{-}\)；
\((2)\)若集合\(A=\{x _{1} , x _{2} , x _{3} , x _{4} \}\)，\(x _{1} < x _{2} < x _{3} < x _{4}\)，且\(A ^{-} =A\)，求证\(x _{1} +x _{4} =x _{2} +x _{3}\)；
\((3)\)若集\(A⊆\{x|0\leqslant x\leqslant 2020.x∈N\}\)，且\(A ^{+} ∩A ^{-} =\varnothing \)，求集合\(A\)中元素的个数的最大值．

查看解析收藏纠错

+选题
题型：解答题题类：期末考试难易度：难
新
年份：2020

已知函数\(f(x)=x ^{m} - \dfrac {4}{x}\)，且\(f(4)=3\)．
\((1)\)求\(m\)的值；
\((2)\)证明\(f(x)\)的奇偶性；
\((3)\)若不等式\(f(x)-a > 0\)在\([1 , +∞)\)上恒成立，求实数\(a\)的取值范围．

查看解析收藏纠错

+选题
题型：解答题题类：期末考试难易度：难
新
年份：2020

非空集合\(A⊆R ^{+}\)，满足\(∀x∈A\)，总有\( \dfrac {1}{x} ∉A\)，记集合\(T(A)=\{(x , y)|x∈A\)，\(y∈A\)，\( \dfrac {x}{y} ∈A\}\)．
\((\)Ⅰ\()\)求证：\(∀x∈A\)，\((x , x)∉T(A)\)；
\((\)Ⅱ\()\)若\(T(A)\)中只有\(1\)个元素\((a , b)\)，求证：\(a=b ^{2}\)；
\((\)Ⅲ\()\)若集合\(A=\{a , b , c , d , e\}\)，且\(a < b < c < d < e\)，\(T(A)\)中恰有\(10\)个元素，求证：\(c ^{2} =ae\)．

查看解析收藏纠错

+选题
题型：解答题题类：期末考试难易度：难
新
年份：2020

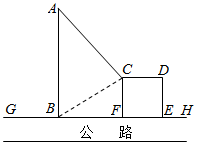如图，\(GH\)是东西方向的公路北侧的边缘线，某公司准备在\(GH\)上的一点\(B\)的正北方向的\(A\)处建一仓库，设\(AB=ykm\)，并在公路北侧建造边长为\(xkm\)的正方形无顶中转站\(CDEF(\)其中边\(EF\)在\(GH\)上\()\)，现从仓库\(A\)向\(GH\)和中转站分别修两条道路\(AB\)，\(AC\)，已知\(AB=AC+1\)，且\(∠ABC=60°\)．
\((1)\)求\(y\)关于\(x\)的函数解析式，并指出定义域；
\((2)\)如果中转站四堵围墙造价为\(1\)万元\(/km\)，两条道路造价为\(3\)万元\(/km\)，问：\(x\)取何值时，该公司建中转站围墙和两条道路总造价\(M\)最低？

查看解析收藏纠错

+选题
题型：解答题题类：期末考试难易度：难
新
年份：2020

已知函数\(f(x)=\log _{a} (1-x)+\log _{a} (x+3)(0 < a < 1)\)
\((1)\)求函数\(f(x)\)的定义域；
\((2)\)求函数\(f(x)\)的零点；
\((3)\)若函数\(f(x)\)的最小值为\(-4\)，求\(a\)的值．

查看解析收藏纠错

+选题
题型：解答题题类：期末考试难易度：难
新
年份：2020

已知\(f(x)=2\sin (2ωx- \dfrac {π}{6})(ω > 0)\)的最小正周期为\(π\)．
\((1)\)求\(ω\)的值，并求\(f(x)\)的单调递增区间；
\((2)\)求\(f(x)\)在区间\([0, \dfrac {5}{12}π]\)上的值域．

查看解析收藏纠错

+选题
题型：解答题题类：期末考试难易度：难
新
年份：2020

设数列\(\{a _{n} \}\)的前\(n\)项和为\(S _{n}\)，\(2S _{n} =a _{n+1} -2 ^{n+1} +1\)，\(n∈N ^{*}\)，且\(a _{1}\)，\(a _{2} +5\)，\(a _{3}\)成等差数列．
\((1)\)证明\(\{ \dfrac {a_{n}}{2^{n}}+1\}\)为等比数列，并求数列\(\{a _{n} \}\)的通项；
\((2)\)设\(b _{n} =\log _{3} (a _{n} +2 ^{n} )\)，且\(T _{n} = \dfrac {1}{b_{1}b_{2}}+ \dfrac {1}{b_{2}b_{3}}+ \dfrac {1}{b_{3}b}_{4}+…+ \dfrac {1}{b_{n}b_{n+1}}\)，证明\(T _{n} < 1\)．
\((3)\)在\((2)\)小问的条件下，若对任意的\(n∈N ^{*}\)，不等式\(b _{n} (1+n)-λn(b _{n} +2)-6 < 0\)恒成立，试求实数\(λ\)的取值范围．

查看解析收藏纠错

+选题
题型：解答题题类：期末考试难易度：难
新
年份：2020

已知函数f（x）=2sin²（+x）-cos2x，x∈[，]．
（Ⅰ）求f（x）的最大值和最小值；
（Ⅱ）若不等式|f（x）-m|＜2在x∈[，]上恒成立，求实数m的取值范围．

查看解析收藏纠错

+选题
题型：解答题题类：期末考试难易度：难
新
年份：2020

已知等差数列\(\{a _{n} \}\)中，公差\(d=2\)，\(a _{2}\)是\(a _{1}\)和\(a _{4}\)的等比中项．
\((1)\)求数列\(\{a _{n} \}\)的通项公式；
\((2)\)设\(b _{n} =|11- \dfrac {1}{2} a _{n} |\)，求数列\(\{b _{n} \}\)的前\(n\)项和\(T _{n}\)．

查看解析收藏纠错

+选题

高中

选择知识点

服务介绍

帮助中心