代数-数学-知识点同步搜题

选择知识点

题型：

全部选择题填空题解答题

难易程度：

全部易较易中档较难难

题类筛选：

全部历年真题模拟题期末考试期中考试月考试卷单元测试其他

年份：

全部 2022 2021 2020 2019 2018 2017 更早

总题量：6262选择本页全部试题

题型：解答题题类：单元测试难易度：难
新
年份：2022

已知函数\( y=\text{sinxcosx}+\sqrt{3}{\mathrm{c}\mathrm{o}\mathrm{s}}^{2}x-\frac{\sqrt{3}}{2},\)求:
(1)函数y的最小正周期;
(2)函数的最大值及取得最大值时x的取值集合;
(3)函数的单调递增区间.

查看解析收藏纠错

+选题
题型：解答题题类：单元测试难易度：难
新
年份：2022

设向量a=(cosx\( ,－\)sinx)\( ,\)b=(2sinx\( ,\)2sinx)\( ,\)且函数f(x)=a⦁b+m的最大值\( \sqrt{2}-1.\)
(1)求实数m的值;
(2)若\( x\in (0,\frac{\pi }{2}),f\left(x\right)=\sqrt{2}-1,\)求x的值.

查看解析收藏纠错

+选题
题型：解答题题类：单元测试难易度：难
新
年份：2022

是否存在角\( a\cdot 3,\alpha \in (-\frac{\pi }{2},\frac{\pi }{2}),\beta \in (0,\pi \))\( ,\)使
\( \{\begin{array}{c}sin(3\pi -a)=\sqrt{2}cos(\frac{\pi }{2}-\beta ),\\ \sqrt{3}cos(-\alpha )=-\sqrt{2}cos(\pi +\beta )\end{array}\)同时成立?若存在\( ,\)求出角α\( ,\)β;若不存在\( ,\)请说明理由.

查看解析收藏纠错

+选题
题型：解答题题类：单元测试难易度：难
新
年份：2022

某货轮在A处看灯塔B在货轮的北偏东\( {75}^{\circ },\)离为\( 12\sqrt{6}nmile,\)在A处看灯塔C在货轮的北偏\( {30}^{\circ },\)距离为\( 8\sqrt{3}nmile,\)货轮由A处向正北航行到D处时\( ,\)再看灯塔B在北偏东120°\( ,\)求:

(1)A处与D处的距离;
(2)灯塔C与D处的距离.

查看解析收藏纠错

+选题
题型：解答题题类：单元测试难易度：难
新
年份：2022

如图:甲、乙两船同时从港口O出发\( ,\)甲船以25海里/小时的速度向东行驶\( ,\)乙船以15海里/小时的速度沿着北偏西30°的方向行驶\( ,\)2小时后\( ,\)甲船到达A处\( ,\)乙船到达B处.求:

(1)甲、乙两船间的距离AB是多少?
(2)此时乙船位于甲船北偏西多少度的方向上?

查看解析收藏纠错

+选题
题型：解答题题类：单元测试难易度：难
新
年份：2022

某海域的东西方向上分别有A\( ,\)B两个观测点如图)\( ,\)它们相距\( 5(3+\sqrt{3})\)海里.现有一艘轮船在D点发出求救信号\( ,\)经探测得知D点位于A点北偏东45°\( ,\)B点北偏西60°\( ,\)这时\( ,\)位于B点南偏西60°且与B点相距\( 20\sqrt{3}\)里的C点有一救援船\( ,\)其航行速度为30海里/小时.

(1)求B点到D点的距离BD;
(2)若命令C处的救援船立即前往D点营救\( ,\)求该救援船到达D点需要的时间.

查看解析收藏纠错

+选题
题型：解答题题类：单元测试难易度：难
新
年份：2022

已知直线l过点(\( －\)2\( ,\)0)\( ,\)当直线l与圆\( {x}^{2}+{y}^{2}\)=2x有两个交点时\( ,\)求直线l斜率k的取值范围.

查看解析收藏纠错

+选题
题型：解答题题类：单元测试难易度：难
新
年份：2022

已知圆\( {x}^{2}+{y}^{2}+x-6y+m=0\)与直线x+2y\( －\)3=0相交于P、Q两点\( ,\)O为原点\( ,\)且\( OP\text{⊥OQ},\)求实数m的值.

查看解析收藏纠错

+选题
题型：解答题题类：单元测试难易度：难
新
年份：2022

求椭圆\( \frac{{x}^{2}}{9}+\frac{{y}^{2}}{16}=1\)上的点到直线l:x+y\( －\)7=0的最短距离.

查看解析收藏纠错

+选题
题型：解答题题类：单元测试难易度：难
新
年份：2022

(14年山东春季高考)如图\( ,{F}_{1}{F}_{2}\)分别是椭圆\( \frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1(a＞0,b＞0)\))的左、右两个焦点\( ,\)且a=\( \sqrt{2}b,M\)为椭圆上一点\( ,M{F}_{2}\)垂直于x轴\( ,\)过\( {F}_{2}\)与OM垂直的直线交椭圆于P\( ,\)Q两点.

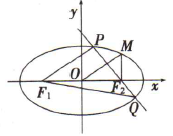
(1)求椭圆的离心率;
(2)若三角形\( P{F}_{1}Q\)的面积为\( 4\sqrt{3},\)求椭圆的标准方程.

查看解析收藏纠错

+选题

高中

选择知识点

服务介绍

帮助中心