题型：解答题 题类：历年真题 难易度：难
年份：2018
题型：解答题 题类：期中考试 难易度：难
年份：2018
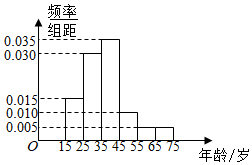2016年6月22日，“国际教育信息化大会”在山东青岛开幕．为了解哪些人更关注“国际教育信息化大会”，某机构随机抽取了年龄在15～75岁之间的100人进行调查，并按年龄绘制频率分布直方图，如图所示，其分组区间为：[15，25），[25，35），[35，45），[45，55），[55，65），[65，75]．把年龄落在区间[15，35）和[35，75]内的人分别称为“青少年”和“中老年”．| 关注 | 不关注 | 合计 | |
| 青少年 | 15 | ||
| 中老年 | |||
| 合计 | 50 | 50 | 100 |
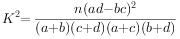，其中n=a+b+c+d| P（K2≥k0） | 0.05 | 0.010 | 0.001 |
| k0 | 3.841 | 6.635 | 10.828 |
在平面直角坐标系xOy中，设椭圆C：
+
=1（a＞b＞0）的下顶点为A，右焦点为F，离心率为
．已知点P是椭圆上一点，当直线AP经过点F时，原点O到直线AP的距离为
是定值． 
，求
的值 
=
．
的值． 
，cn=f（2n+4）（n∈N*），求数列{cn}的前n项和Tn．
．
为等差数列；
如图，椭圆E：
（a＞b＞0）的左、右焦点分别为F1，F2，MF2⊥x轴，直线MF1交y轴于H点，OH=
，Q为椭圆E上的动点，△F1F2Q的面积的最大值为1．