选择章节

如图，在直三棱柱\(ABC-{{A}_{1}}{{B}_{1}}{{C}_{1}}\)中，\(D\)，\(E\)分别为\(AB\)，\(BC\)的中点，点\(F\)在侧棱\({B}{{{B}}_{{1}}}\)上，且\({{B}_{1}}D\bot {{A}_{1}}F,{{A}_{1}}{{C}_{1}}\bot {{A}_{1}}{{B}_{1}}\)。

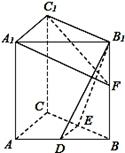
\((1)\)若平面\({A}_{1}{C}_{1}F∩ \)平面\(DEB_{1}=\)直线\(l\)，求证\(DE/\!/l\)；

\((2)\)若\(AC=AB=A{{A}_{1}}=2\)，求点\(E\)到平面\({{A}_{1}}{{C}_{1}}F\)的距离。

如图，在长方体\(ABCD-{A}_{1}{B}_{1}{C}_{1}{D}_{1} \)中，\(D{D}_{1}=AD=2 \)，\(DC=4\)，过\(D\)作\(DF⊥{D}_{1}B \)交\(D_{1}B\)于点\(F\)，\(E\)是\(CD_{1}\)上一点。

\((\)Ⅰ\()\)若\(BC/\!/ \)平面\(DEF\)，求证：\(EC=5D_{1}E\)；

\((\)Ⅱ\()\)在\((\)Ⅰ\()\)的条件下，求三棱锥\({D}_{1}-DEF \)的体积。

如图，已知\(AB\)为圆\(O\)的直径，\(C\)为圆上一动点，\(PA⊥\)圆\(O\)所在的平面，且\(PA=AB=2\)，过点\(A\)作平面\(α⊥PB\)，分别交\(PB\)，\(PC\)于\(E\)，\(F\)，当三棱锥\(P-AEF\)的体积最大时，\(\tan ∠BAC=\)(    )