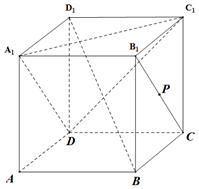
如图,在正方体\(ABCD-A _{1} B _{1} C _{1} D _{1}\)中,点\(P\)在线段\(B _{1} C\)上运动,则下列命题:
①直线\(BD _{1} ⊥\)平面\(A _{1} C _{1} D\);
②三棱锥\(P-A _{1} C _{1} D\)的体积为定值;
③异面直线\(AP\)与\(A _{1} D\)所成角的取值范围是\([45° , 90°]\);
④直线\(C _{1} P\)与平面\(A _{1} C _{1} D\)所成角的正弦值的最大值为\( \dfrac { \sqrt {6}}{3}\).
其中所有真命题的序号是______.
 如图,在正方体\(ABCD-A _{1} B _{1} C _{1} D _{1}\)中,点\(P\)在线段\(B _{1} C\)上运动,则下列命题:
如图,在正方体\(ABCD-A _{1} B _{1} C _{1} D _{1}\)中,点\(P\)在线段\(B _{1} C\)上运动,则下列命题: