选择章节

\([2021\)湖南师大附中高一期末\(]\)已知函数\(f(x)\)是偶函数，且当\(x\geqslant 0\)时，\(f(x)=\log_{a}(3-ax)(a>0,\)且\(a≠1)\)，________.

\((1)\)求当\(x< 0\)时，\(f(x)\)的解析式；

\((2)\)在①\(f(x)\)在\((1,4)\)上单调递增，②在区间\((-1,1)\)上恒有\(f(x)\geqslant x^{2}\)这两个条件中任选一个补充到上面的横线中，求\(g(a)={(\dfrac{1}{2})}^{a}\)的值域．
注：如果选择多个条件分别解答，则按第一个解答记分.

已知函数\(f(x)\)是偶函数，且当\(x⩾0\)时，\(f(x)={\log}_{a}\;(3-ax)(a>0,\)且\(a\neq 1).\)

\((1)\)求当\(x< 0\)时的\(f(x)\)的解析式；

\((2)\)在①\(f(x)\)在\(\left(1,4\right)\)上单调递增；②在区间\(\left(-1,1\right)\)上恒有\(f(x)⩾{x}^{2}\)这两个条件中任选一个补充到本题中，求\(g(a)={(\dfrac{1}{2})}^{a}\)的取值范围\(.(\)注：如果选择多个条件分别解答，则按第一个解答计分\().\)

\((1)\)若\(f(1)=1\)，求\(f\left(x\right)\)的单调区间．

\((2)\)是否存在实数\(a\)，使\(f\left(x\right)\)的最小值为\(0?\)若存在，求出\(a\)的值；若不存在，请说明理由．

\([2021\)湖南师大附中高一期末\(]\)已知函数\(f(x)\)是偶函数，且当\(x\geqslant 0\)时，\(f(x)=\log_{a}(3-ax)(a>0,\)且\(a≠1)\)，________.

\((1)\)求当\(x< 0\)时，\(f(x)\)的解析式；

\((2)\)在①\(f(x)\)在\((1,4)\)上单调递增，②在区间\((-1,1)\)上恒有\(f(x)\geqslant x^{2}\)这两个条件中任选一个补充到上面的横线中，求\(g(a)={{(\dfrac{1}{2})}^{a}}\)的值域．

注：如果选择多个条件分别解答，则按第一个解答计分．

\([2021\)巴蜀中学高一期末\(]\)已知函数\(f(x)={{\log}_{\frac{1}{3}}}(x+1).\)

\((1)\)求函数\(y=f(x)+f(2-x)\)的定义域；

\((2)\)设\(g(x)={{\log}_{\frac{1}{3}}}({{x}^{2}}-3x+12)-f(x)\)，若函数\(g(x)\)在区间\((1,m]\)上的最大值为\(-1\)，求实数\(m\)的取值范围．

\([2021\)南充高级中学高一期中\(]\)某校园“文化长廊”酷似抛物线图象的一部分\((\)图\(1)\)，尺寸如图所示\((\)单位：\(m)\)，建立如图\(2\)所示的坐标系，\(O\)为坐标原点，设该抛物线方程为\(f(x)=-x^{2}+bx+c(x\in\)\(R\)\()\)，其图象交\(x\)轴于\(O\)，\(A\)两点，\(OA=3.\)

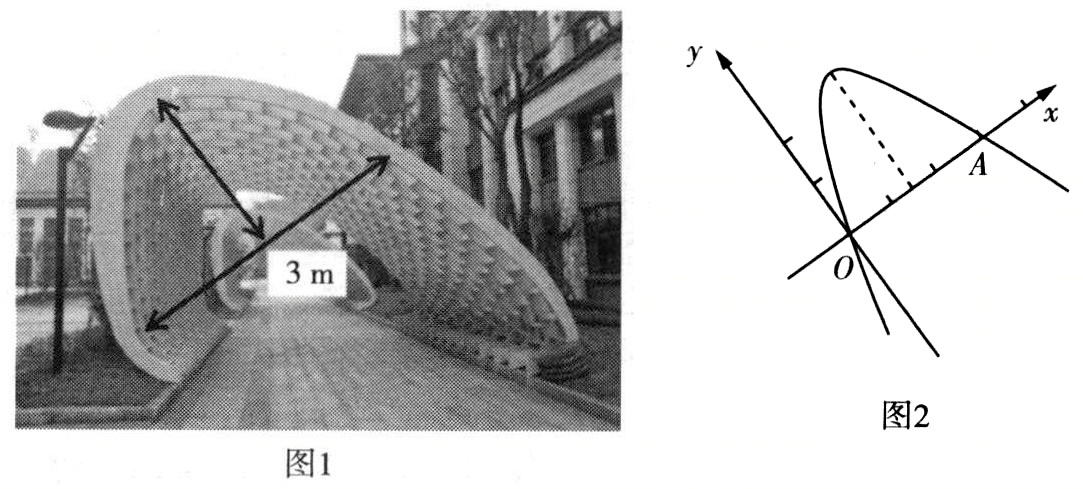
\((1)\)求\(f(x)\)的解析式；

\((2)\)求函数\(g(x)={{2}^{f(x)-\frac{5}{4}}}\)的单调区间及值域．

设函数\(f\left(x\right)=\lg\left({{a}^{x}}-{{b}^{x}}\right)\)，其中\(a>0\)，\(b>0\)且\(a\neq b.\)

\((Ⅰ)\)求\(f\left(x\right)\)的定义域；

\((Ⅱ)\)当\(a>1>b>0\)时，函数\(f\left(x\right)\)图象上是否存在不同两点，使过这两点的直线平行于\(x\)轴，并证明．

已知函数\(f\left(x\right)={{3}^{{{x}^{2}}-2x}}.\)

\((1)\)求函数\(f\left(x\right)\)的单调区间；

\((2)\)当\(x\)取何值时，函数\(f\left(x\right)\)取得最小值，并求出最小值．