代数-数学-知识点同步搜题

选择知识点

题型：

全部选择题填空题解答题

难易程度：

全部易较易中档较难难

题类筛选：

全部历年真题模拟题期末考试期中考试月考试卷单元测试其他

年份：

全部 2022 2021 2020 2019 2018 2017 更早

总题量：68选择本页全部试题

题型：选择题题类：期末考试难易度：较难
新测
年份：2020

在平面直角坐标系\(xOy\)中，已知\(A\)，\(B\)为圆\(C\)：\((x-m) ^{2} +(y-2) ^{2} =4\)上两个动点，且\(|AB|=2 \sqrt {3}\)，若直线\(l\)：\(y=-2x\)上存在点\(P\)，使得\( \overrightarrow {OC}= \overrightarrow {PA}+ \overrightarrow {PB}\)，则实数\(m\)的取值范围为\((\:\:\:\:)\)

A.\([1- \sqrt {5},1+ \sqrt {5}]\) B.\([- \sqrt {5}-1,- \sqrt {5}+1]\) C.\([ \sqrt {5}-1, \sqrt {5}+1]\) D.\([-1- \sqrt {5},-1+ \sqrt {5}]\)

查看解析收藏纠错

+选题
题型：选择题题类：期末考试难易度：较难
新测
年份：2020

已知函数\(f(x)\)的定义域为\(\text{R}\)，且\(f(x+1)\)是偶函数，\(f(x-1)\)是奇函数，\(f(x)\)在\([-1,1]\)上单调递增，则\((\) \()\)

A.\(f(0) > f(2020) > f(2019)\) B.\(f(0) > f(2019) > f(2020)\) C.\(f(2020) > f(2019) > f(0)\) D.\(f(2020) > f(0) > f(2019)\)

查看解析收藏纠错

+选题
题型：选择题题类：期末考试难易度：较难
新测
年份：2020

如图，网格纸上小正方形的边长为\(1\)，粗实线画出的是某几何体的三视图，则该几何体外接球的表面积是\((\:\:\:\:)\)

A.\(41π\) B.\( \dfrac {41}{4}π\) C.\(25π\) D.\( \dfrac {25}{4}π\)

查看解析收藏纠错

+选题
题型：选择题题类：期末考试难易度：较难
新测
年份：2020

若不等式对任意的x∈（-∞，0]恒成立，则a的取值范围是（）

A.（-∞，2] B.（-∞，1] C.[1，＋∞） D.[2，＋∞）

查看解析收藏纠错

+选题
题型：选择题题类：期末考试难易度：较难
新测
年份：2020

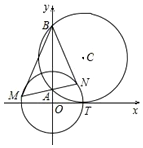如图，圆\(C\)与\(x\)轴相切于点\(T(1 , 0)\)，与\(y\)轴正半轴交于两点\(A\)，\(B(B\)在\(A\)的上方\()\)，且\(|AB|=2.\)过点\(A\)任作一条直线与圆\(O\)：\(x ^{2} +y ^{2} =1\)相交于\(M\)，\(N\)两点，\( \dfrac {|NB|}{|NA|}+ \dfrac {|MA|}{|MB|}\)的值为\((\:\:\:\:)\)

A.\(2\) B.\(3\) C.\(2 \sqrt {2}\) D.\( \sqrt {2}-1\)

查看解析收藏纠错

+选题
题型：选择题题类：期末考试难易度：较难
新测
年份：2020

已知定义在\(R\)上的函数\(f(x)= \dfrac {2^{1-x}-2^{x-1}}{2^{1-x}+2^{x-1}} -(x-1) ^{3}\)，则不等式\(f(2x+3)+f(x-2)\geqslant 0\)的解集为\((\:\:\:\:)\)

A.\((-∞ , \dfrac {1}{3} ]\) B.\((0 , \dfrac {1}{3} ]\) C.\((-∞ , 3]\) D.\((0 , 3]\)

查看解析收藏纠错

+选题
题型：选择题题类：期末考试难易度：较难
新测
年份：2020

将函数\(y=\sin x\)的图象向右平移\( \dfrac {π}{6}\)个单位长度，再将横坐标缩短为原来的\( \dfrac {1}{\omega } (ω > 0)\)得到函数\(y=f(x)\)的图象，若\(y=f(x)\)在\([0 , \dfrac {π}{6} ]\)上的最大值为\( \dfrac {ω}{5}\)，则\(ω\)的取值个数为\((\:\:\:\:)\)

A.\(1\) B.\(2\) C.\(3\) D.\(4\)

查看解析收藏纠错

+选题
题型：选择题题类：期末考试难易度：较难
新测
年份：2020

已知双曲线，直线l过其左焦点F₁，交双曲线左支于A、B两点，且|AB|=4，F₂为双曲线的右焦点，△ABF₂的周长为20，则m的值为（　　）

A.8 B.9 C.16 D.20

查看解析收藏纠错

+选题
题型：选择题题类：期末考试难易度：较难
新测
年份：2020

已知\(f(x)= \begin{cases} (2a-1)x+4a,x\leqslant 1 \\ \log _{a}x,x > 1\end{cases}\)是\((-∞ , +∞)\)上的减函数，则\(a\)的取值范围是\((\:\:\:\:)\)

A.\((0 , 1)\) B.\((0 , \dfrac {1}{2} )\) C.\(( \dfrac {1}{6}, \dfrac {1}{2} )\) D.\([ \dfrac {1}{6}, \dfrac {1}{2} )\)

查看解析收藏纠错

+选题
题型：选择题题类：期末考试难易度：较难
新测
年份：2020

已知函数\(f(x)=\{\begin{matrix}\begin{matrix}−{x}^{2}+2x,x\leqslant 0 \\ \ln (x+1),x > 0\end{matrix}\end{matrix}\)，若\(|f(x)|\geqslant 2ax\)，则\(a\)的取值范围是\((\:\:\:\:)\)

A.\((-∞ , 0]\) B.\([-2 , 1]\) C.\([-2 , 0]\) D.\([-1 , 0]\)

查看解析收藏纠错

+选题

高中

选择知识点

服务介绍

帮助中心