题型：填空题 题类：模拟题 难易度：较易
新年份：2020
如图，在矩形\(ABCD\)中，\(BC=2AB=2\)，\(N\)为\(BC\)的中点，将\(\triangle ABN\)沿\(AN\)翻折成\(\triangle B _{1} AN(B _{1} ∉\)平面\(ABCD)\)，\(M\)为线段\(B _{1} D\)的中点，则在\(\triangle ABN\)翻折过程中给出以下四个结论：题型：填空题 题类：模拟题 难易度：较易
新年份：2020
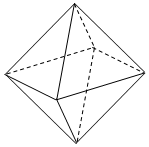已知柏拉图多面体是指每个面都是全等的正多边形构成的凸多面体．著名数学家欧拉研究并证明了多面体的顶点数\((V)\)、棱数\((E)\)、面数\((F)\)之间存在如下关系：\(V+F-E=2.\)利用这个公式，可以证明柏拉图多面体只有\(5\)种，分别是正四面体、正六面体\((\)正方体\()\)、正八面体、正十二面体和正二十面体．若棱长相等的正六面体和正八面体\((\)如图\()\)的外接球的表面积分别为\(S _{1}\)，\(S _{2}\)，则\( \dfrac {S_{1}}{S_{2}}\)的值为______． 
某中学为了了解高三年级女生的体重\((\)单位：千克\()\)情况，从中随机抽测了\(100\)名女生的体重，所得数据均在区间\([48 , 58]\)中，其频率分布直方图如图所示，则在抽测的\(100\)名女生中，体重在区间\([50 , 56]\)的女生数为______． 