(2019•山东) (本小题8分) 如图所示,已知椭圆\( \frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1(a>b>0)\)的两个焦点分别是F
1,F
2,短轴的两个端点分别是B
1,B
2,四边形F
1B
1F
2B
2,为正方形,且椭圆经过点\( P\left(1,\frac{\sqrt{2}}{2}\right)\)。
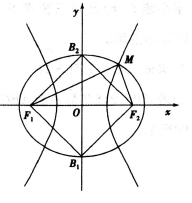
(1)求椭圆的标准方程;
(2)与椭圆有公共点的双曲线,其离心率\( e=\frac{3\sqrt{2}}{2}\),且与椭圆在第一象限交于点M。求线段 MF
1,MF
2,的长度。
