题型：解答题 题类：历年真题 难易度：较难
新年份：2019
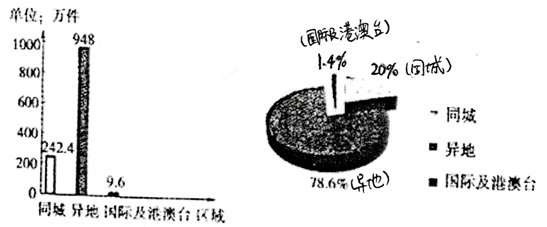
(1)2018年3～12月该市邮政快递同城业务量完成件数与2017年3～12月相比是有所增大还是有所减少，并计算，2018年3～12月该市邮政快递国际及港澳台业务量同比增长率：
(2)若年平均每件快递的盈利如表所示：
快递类型 | 同城 | 异地 | 国际及港澳台 |
盈利(元／件) | 0.5 | 5 | 25 |
估计该市邮政快递在2018年3～12月的盈利是多少?
题型：解答题 题类：历年真题 难易度：较难
新年份：2019
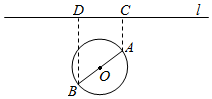如图，一个湖的边界是圆心为O的圆，湖的一侧有一条直线型公路l，湖上有桥AB（AB是圆O的直径）．规划在公路l上选两个点P、Q，并修建两段直线型道路PB、QA，规划要求：线段PB、QA上的所有点到点O的距离均不小于圆O的半径．已知点A、B到直线l的距离分别为AC和BD（C、D为垂足），测得AB=10，AC=6，BD=12（单位：百米）．
+
=1（a＞b＞0）上的一点，则过点P的椭圆的切线方程为
．已知椭圆C：
，过椭圆C外一点M（x0，y0）作椭圆的两条切线MA，MB（A，B为切点）．
． 
＝﹣2；
，且△ABC的面积为
，求c．
时，角A的大小．
．
，
，
，
． 
已知椭圆C：
，（a＞b＞0）过点（1，
）且离心率为
的焦距为4，点P（2，3）在椭圆上．
的两条切线PA，PB，切线PA，PB与椭圆C的另一个交点分别为A，B，试问直线AB的斜率是否为定值？若是，求出其定值，若不是，请说明理由． 
（θ为参数）．以原点O为极点，x轴的正半轴为极轴，建立极坐标系，直线l的极坐标方程为
（t∈R）.