代数-数学-知识点同步搜题

选择知识点

题型：

全部选择题填空题解答题

难易程度：

全部易较易中档较难难

题类筛选：

全部历年真题模拟题期末考试期中考试月考试卷单元测试其他

年份：

全部 2022 2021 2020 2019 2018 2017 更早

总题量：68选择本页全部试题

题型：解答题题类：历年真题难易度：难
新
年份：2020

已知椭圆C：的短轴长为2，离心率为，左顶点为A，过点A的直线l与C交于另一个点M，且与直线x=t交于点N．
（1）求椭圆C的方程；
（2）是否存在实数t，使得为定值？若存在，求实数t的值；若不存在，请说明理由．

查看解析收藏纠错

+选题
题型：解答题题类：历年真题难易度：难
新
年份：2020

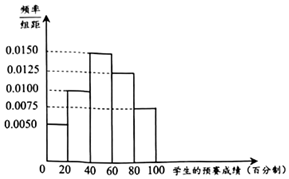某市为提升中学生的数学素养，激发学生学习数学的兴趣，举办了一次“数学文化知识大赛”，分预赛和复赛两个环节．已知共有8000名学生参加了预赛，现从参加预赛的全体学生中随机地抽取100人的预赛成绩作为样本，得到如下频率分布直方图．
（1）规定预赛成绩不低于80分为优良，若从上述样本中预赛成绩不低于60分的学生中随机地抽取2人，求恰有1人预赛成绩优良的概率；
（2）由频率分布直方图可认为该市全体参加预赛学生的预赛成绩Z服从正态分布N（μ，σ²），其中μ可近似为样本中的100名学生预赛成绩的平均值（同一组数据用该组区间的中点值代替），且σ²=362．利用该正态分布，估计全市参加预赛的全体学生中预赛成绩不低于91分的人数；
（3）预赛成绩不低于91分的学生将参加复赛，复赛规则如下：①每人的复赛初始分均
为100分；②参赛学生可在开始答题前自行决定答题数量n，每一题都需要“花”掉（即减去）一定分数来获取答题资格，规定答第k题时“花”掉的分数为0.1k（k（=1，2n））；
③每答对一题加1.5分，答错既不加分也不减分；④答完n题后参赛学生的最终分数即为复赛成绩．已知学生甲答对每道题的概率均为0.7，且每题答对与否都相互独立．若学生甲期望获得最佳的复赛成绩，则他的答题数量n应为多少？
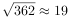（参考数据：；若Z～N（μ，σ²），则P（μ-σ＜Z＜μ+σ）≈0.6827，P（μ-2σ＜Z＜μ+2σ）≈0.9545，P（μ-3σ＜Z＜μ+3σ）≈0.9973．

查看解析收藏纠错

+选题
题型：解答题题类：历年真题难易度：难
新
年份：2020

设等差数列{a_n}的首项为0，公差为a，a∈N*；等差数列{b_n}的首项为0，公差为b，b∈N*．由数列{a_n}和{b_n}构造数表M，与数表M*：
记数表M中位于第i行第j列的元素为c_i，j，其中c_i，j=a_i+b_j（i，j=1，2，3，…）．
记数表M*中位于第i行第j列的元素为d_i，j，其中d_i，j=a_i-b_j+1．（1≤i≤b，i∈N*，j∈N*）．如：c_1，2=a₁+b₂，d_l，2=a₁-b₃．
（I）设a=5，b=9，请计算c_2，6，c_396，6，d_2，6；
（Ⅱ）设a=6．b=7，试求c_i，j，d_i，j的表达式（用i，j表示），并证明：对于整数t，若t不属于数表M，则t属于数表M*；
（Ⅲ）设a=6，b=7，对于整数t，t不属于数表M，求t的最大值．

查看解析收藏纠错

+选题
题型：解答题题类：历年真题难易度：难
新
年份：2020

已知数列{a_n}是由正整数组成的无穷数列．若存在常数k∈N^*，使得a_2n-1+a_2n=ka_n对任意的n∈N^*成立，则称数列{a_n}具有性质Ψ（k）．
（Ⅰ）分别判断下列数列{a_n}是否具有性质Ψ（2）；（直接写出结论）
①a_n=1；②a_n=2ⁿ．
（Ⅱ）若数列{a_n}满足a_n+1≥a_n（n=1，2，3，…），求证：“数列{a_n}具有性质Ψ（2）”是“数列{a_n}为常数列”的充分必要条件；
（Ⅲ）已知数列{a_n}中a₁=1，且a_n+1＞a_n（n=1，2，3，…）．若数列{a_n}具有性质Ψ（4），求数列{a_n}的通项公式．

查看解析收藏纠错

+选题
题型：解答题题类：历年真题难易度：难
新
年份：2020

四面体A-BCD中，O，E分别是BD，BC的中点，AC=BC=CD=BD=2，AB=AD=
（1）求证：AO⊥平面BCD；
（2）求异面直线AB与CD所成角的余弦值；
（3）求点C到平面AED的距离．

查看解析收藏纠错

+选题
题型：解答题题类：历年真题难易度：难
新
年份：2020

已知椭圆C的中心在坐标原点O，其右焦点为F（1，0），以坐标原点O为圆心，椭圆短半轴长为半径的圆与直线x-y+=0的相切．
（1）求椭圆C的方程；
（2）经过点F的直线l₁，l₂分别交椭圆C于A、B及C、D四点，且l₁⊥l₂，探究：是否存在常数λ，使|AB|+|CD|=λ|AB|•|CD|恒成立．

查看解析收藏纠错

+选题
题型：解答题题类：历年真题难易度：难
新
年份：2020

已知椭圆P的中心O在坐标原点，焦点在x轴上，且经过点A（0，2），离心率为
（1）求椭圆P的方程；
（2）是否存在过点E（0，-4）的直线l交椭圆P于点R，T，且满足•=．若存在，求直线l的方程；若不存在，请说明理由．

查看解析收藏纠错

+选题
题型：解答题题类：历年真题难易度：难
新
年份：2020

已知三棱柱ABC-A₁B₁C₁中，M、N分别是CC₁与A₁B的中点，△ABA₁为等边三角形，CA=CA₁，A₁A=A₁M=2BC．

（Ⅰ）求证：MN∥平面ABC；
（Ⅱ）（i）求证：BC⊥平面ABB₁A₁；
（ii）求二面角A-MN-B的正弦值．

查看解析收藏纠错

+选题
题型：解答题题类：历年真题难易度：难
新
年份：2020

(2020•山东)已知点E，F分别是正方形ABCD的边AD.BC的中点.现将四边形EFCD
沿EF折起，使二面角C-EF-B为直二面角，如图所示.
(1)若点G，H分别是AC，BF的中点，求证:GH∥平面EFCD;
(2)求直线AC与平面ABFE所成角的正弦值.

查看解析收藏纠错

+选题
题型：解答题题类：历年真题难易度：难
新
年份：2020

(2020•山东)已知抛物线的顶点在坐标原点O，椭圆\( \frac{{x}^{2}}{4}+{y}^{2}=1\)的顶点分别为\( {A}_{1}\)，\( {A}_{2}\)，\( {B}_{1}\)，\( {B}_{2}\)，其中点\( {A}_{2}\)为抛物线的焦点，如图所示.
(1)求抛物线的标准方程;
(2)若过点\( {A}_{1}\)的直线\( l\)与抛物线交于M，N两点，且\( (\overrightarrow{OM}+\overrightarrow{ON})//\overline{{B}_{1}{A}_{2}}\)，求直线\( l\)的方程.

查看解析收藏纠错

+选题

高中

选择知识点

服务介绍

帮助中心