题型：解答题 题类：期中考试 难易度：较易
新年份：2021
设椭圆\(E\)：\(\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1\left(a>b>0\right)\)的左焦点为\(F\)，离心率为\(\dfrac{\sqrt{3}}{3}\)，过点\(F\)且与\(x\)轴垂直的直线被椭圆截得的线段长为\(\dfrac{4\sqrt{3}}{3}.\)
\((1)\)求椭圆\(E\)的方程；
\((2)\)设\(A\)，\(B\)分别为椭圆\(E\)的左、右顶点，过点\(F\)且斜率为\(k\)的直线与椭圆\(E\)交于点\(C\)，\(D\)两点，且\(\overrightarrow{AC}⋅\overrightarrow{DB}+\overrightarrow{AD}⋅\overrightarrow{CB}=\dfrac{52}{7}\)，求\(k\)的值．
题型：解答题 题类：期中考试 难易度：较易
新年份：2021
题型：解答题 题类：期中考试 难易度：较易
新年份：2021
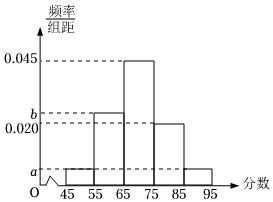第\(19\)届亚运会将于\(2022\)年\(9\)月在杭州举行，志愿者的服务工作是亚运会成功举办的重要保障．某高校承办了杭州志愿者选拔的面试工作．现随机抽取了\(100\)名候选者的面试成绩，并分成五组：第一组\([45,55),\)第二组\([55,65),\)第三组\([65,75),\)第四组\([75,85),\)第五组\([85,95),\)绘制成如图所示的频率分布直方图．已知第三、四、五组的频率之和为\(0.7\)，第一组和第五组的频率相同．
