题型:填空题 题类:其他 难易度:难
年份:2018
\((1)\)将\(5\)位志愿者分到世博会的\(4\)个不同场馆服务,每位志愿者去一个场馆,每个场馆至少安排一位志愿者,则不同的安排方案有________种.
\((2)\)一只蚂蚁位于数轴\(x=0\)处,这只蚂蚁每隔一秒钟向左或向右移动一个单位,设它向右移动的概率为\( \dfrac{2}{3}\),向左移动的概率为\( \dfrac{1}{3}\),则\(3\)秒后,这只蚂蚁在\(x=1\)处的概率为_________.
\((3){\left(x+1\right)}^{3}+{\left(x-2\right)}^{8}={a}_{0}+{a}_{1}\left(x-1\right)+{a}_{2}{\left(x-1\right)}^{2}+⋯+{a}_{8}{\left(x-1\right)}^{8} \),则\({{a}_{2}}=\)_________.
\((4)\)若对\(∀{x}_{1}∈(0,2] ,∃{x}_{2}∈[1,2] \),使\(4{{x}_{1}}\ln {{x}_{1}}-x_{1}^{2}+3+4{{x}_{1}}x_{2}^{2}+8a{{x}_{1}}{{x}_{2}}-18{{x}_{1}}\geqslant 0\)成立,则实数\(a \)的取值范围是____________.
题型:填空题 题类:其他 难易度:难
年份:2018
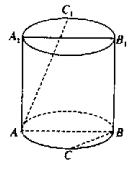
\((1)\)圆台的较小底面半径为\(1\),母线长为\(2\),一条母线和底面的一条半径有交点且成\(60{}^\circ \)角,则圆台的侧面积为____________
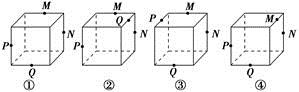
\((2)\)如图所示的正方体中,\(P\),\(Q\),\(M\),\(N\)分别是所在棱的中点,则这四个点共面的图形是________\((\)把正确图形的序号都填上\()\).
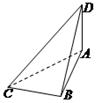
\((3)\)如图,已知球\(O\)的面上四点\(A\)、\(B\)、\(C\)、\(D\),\(DA⊥\)平面\(ABC\),\(AB⊥BC\),\(DA=AB=BC=\sqrt{3}\),则球\(O\)的体积等于______.