代数-数学-知识点同步搜题

选择知识点

题型：

全部选择题填空题解答题

难易程度：

全部易较易中档较难难

题类筛选：

全部历年真题模拟题期末考试期中考试月考试卷单元测试其他

年份：

全部 2022 2021 2020 2019 2018 2017 更早

总题量：3107选择本页全部试题

题型：解答题题类：模拟题难易度：较易
新
年份：2021

在\(\triangle ABC\)中，角\(A\)，\(B\)，\(C\)所对的边分别为\(a\)，\(b\)，\(c.\)且满足\(\cos(A-B)+\cos C=\sqrt{3}\sin(A-B)+\sqrt{3}\sin C.\)
\((1)\)求\(B\)的大小；
\((2)\)若\(b=2\)，求\(\triangle ABC\)面积的最大值．

查看解析收藏纠错

+选题
题型：解答题题类：模拟题难易度：较易
新
年份：2021

已知正项数列\(\{a_{n}\}\)的前\(n\)项和为\(S_{n}\)，且\(a_{1}=2\)，\(2S_{n}=(a_{n}+2)(2a_{n}-3).\)
\((1)\)求数列\(\{a_{n}\}\)的通项公式；
\((2)\)若数列\(\{b_{n}\}\)满足\(b_{n}=\dfrac{1}{a_{n+1}\sqrt{a_{n}}}\)，其前\(n\)项和为\(T_{n}\)，证明：\(T_{n}< 2\sqrt{2}-\dfrac{4\sqrt{2}}{\sqrt{n+4}}.\)

查看解析收藏纠错

+选题
题型：解答题题类：模拟题难易度：较易
新
年份：2021

已知函数\(f(x)=\log_{k}x(k\)为常数，\(k>0\)且\(k≠1).\)
\((1)\)在下列条件中选择一个，使数列\(\{a_{n}\}\)是等比数列，并说明理由．
①数列\(\{f(a_{n})\}\)是首项为\(2\)，公比为\(2\)的等比数列；
②数列\(\{f(a_{n})\}\)是首项为\(4\)，公差为\(2\)的等差数列；
③数列\(\{f(a_{n})\}\)是首项为\(2\)，公差为\(2\)的等差数列的前\(n\)项和构成的数列．
\((2)\)在\((1)\)的条件下，当\(k=\sqrt{2}\)时，设\(b_{1}=a_{1}\)，\(b_{n}=na_{n}-(n-1)a_{n-1}\)，\((n\geqslant 2,n\in N^{*})\)，求数列\(\{b_{n}\}\)的前\(n\)项和\(T_{n}.\)

查看解析收藏纠错

+选题
题型：解答题题类：模拟题难易度：较易
新
年份：2021

已知椭圆\(Ω\)：\(\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1(a>b>0)\)的左、右焦点分别为\(F_{1}\)，\(F_{2}\)，离心率为\(\dfrac{1}{2}\)，\(P\)为椭圆\(Ω\)上的动点，且满足\(\overrightarrow {PF_{1}}\cdot\overrightarrow {PF_{2}}\)的最大值为\(3.\)
\((1)\)求椭圆\(Ω\)的标准方程；
\((2)\)过椭圆\(Ω\)的右焦点\(F_{2}\)的直线\(l\)与椭圆\(Ω\)交于\(A\)，\(B\)两点，若原点\(O\)为\(\triangle ABC\)的重心，当\(\triangle ABC\)的面积\(S=\dfrac{18\sqrt{2}}{7}\)时，求直线\(l\)的方程．

查看解析收藏纠错

+选题
题型：解答题题类：模拟题难易度：较易
新
年份：2021

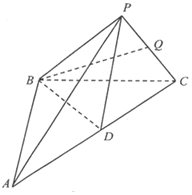如图，在三棱锥\(P-ABC\)中，\(AB=BC\)，\(AP=PC\)，\(∠ABC=60°\)，\(AP⊥PC\)，直线\(BP\)与平面\(ABC\)成\(30°\)角，\(D\)为\(AC\)的中点，\(\overrightarrow {PQ}=λ\overrightarrow {PC}\)，\(λ\in(0,1).\)
\((Ⅰ)\)若\(PB>PC\)，求证：平面\(ABC⊥\)平面\(PAC\)；
\((Ⅱ)\)若\(PB< PC\)，求直线\(BQ\)与平面\(PAB\)所成角的正弦值的取值范围．

查看解析收藏纠错

+选题
题型：解答题题类：模拟题难易度：较易
新
年份：2021

在锐角三角形\(\triangle ABC\)中，角\(A\)、\(B\)、\(C\)的对边分别为\(a\)、\(b\)、\(c\)，\(b\cos(\dfrac{π}{2}-A)-\sqrt{3}a\cos B=0.\)
\((Ⅰ)\)求角\(B\)的值；
\((Ⅱ)\)若\(\sqrt{3}(a^{2}+c^{2}-b^{2})-abc=0\)，求\(\triangle ABC\)面积的取值范围．

查看解析收藏纠错

+选题
题型：解答题题类：模拟题难易度：较易
新
年份：2021

已知数列\(\{a_{n}\}\)是正项等比数列，满足\(a_{3}\)是\(2a_{1}\)，\(3a_{2}\)的等差中项，\(a_{4}=16.\)
\((1)\)求数列\(\{a_{n}\}\)的通项公式；
\((2)\)若\(b_{n}=(-1)^{n}\log_{2}a_{2n+1}\)，求数列\(\{b_{n}\}\)的前\(n\)项和\(T_{n}.\)

查看解析收藏纠错

+选题
题型：解答题题类：模拟题难易度：较易
新
年份：2021

在\(\triangle ABC\)中，角\(A\)，\(B\)，\(C\)所对边长分别为\(a\)，\(b\)，\(c\)，已知\(6\sin C\cos A=7\sin 2A\)，且\(5a=3b.\)
\((Ⅰ)\)求\(C\)；
\((Ⅱ)\)若\(\triangle ABC\)的面积\(S=15\sqrt{3}\)，求\(c.\)

查看解析收藏纠错

+选题
题型：解答题题类：模拟题难易度：较易
新
年份：2021

在\(\triangle ABC\)中，\(a\)、\(b\)、\(c\)分别是内角\(A\)、\(B\)、\(C\)的对边，以下三个条件任选一个作答，如果选择多个条件分别解答，按第一个解答计分．
①\(\dfrac{a}{\cos A},\dfrac{b}{\cos A},\dfrac{c}{\cos C}\)成等差数列；
②\(2a-b=2c\cos B\)；
③\(c\cos(B-A)+c\cos C=2\sqrt{3}b\sin A\cos C\)；
\((1)\)求角\(C\)的大小；
\((2)\)若\(c=2\sqrt{3}\)，\(\triangle ABC\)的面积为\(\sqrt{3}\)，求\(a+b\)和\(\sin A+\sin B\)的值．

查看解析收藏纠错

+选题
题型：解答题题类：模拟题难易度：较易
新
年份：2021

已知数列\(\{a_{n}\}\)，\(a_{n}=(a_{n-1})^{\frac{n}{n-1}}(n\geqslant 2)\)，\(a_{1}=e.\)
\((1)\)求\(a_{n}\)；
\((2)\)求\(a_{1}+2a_{2}+3a_{3}+⋯+10a_{10}.\)

查看解析收藏纠错

+选题

高中

选择知识点

服务介绍

帮助中心