题型:解答题 题类:历年真题 难易度:较易
新年份:2021
某厂研制了一种生产高精产品的设备,为检验新设备生产产品的某项指标有无提高,用一台旧设备和一台新设备各生产了\(10\)件产品,得到各件产品该项指标数据如下:
旧设备 | \(9\text{.}8\) | \(10\text{.}3\) | \(10\text{.}0\) | \(10\text{.}2\) | \(9\text{.}9\) | \(9\text{.}8\) | \(10\text{.}0\) | \(10\text{.}1\) | \(10\text{.}2\) | \(9\text{.}7\) |
新设备 | \(10\text{.}1\) | \(10\text{.}4\) | \(10\text{.}1\) | \(10\text{.}0\) | \(10\text{.}1\) | \(10\text{.}3\) | \(10\text{.}6\) | \(10\text{.}5\) | \(10\text{.}4\) | \(10\text{.}5\) |
旧设备和新设备生产产品的该项指标的样本平均数分别记为\(\bar{x}\text{和}\bar{y}\),样本方差分别记为\(s_{1}^{2}\)和\(s_{2}^{2}.\)
\((1)\)求\(\bar{x}\text{,}\bar{y}\text{,}s_{1}^{2}\text{,}s_{2}^{2}\);
\((2)\)判断新设备生产产品的该项指标的均值较旧设备是否有显著提高\((\)如果\(\bar{y}-\bar{x}\text{⩾}2\sqrt{\dfrac{s_{1}^{2}\text{+}s_{2}^{2}}{10}}\),则认为新设备生产产品的该项指标的均值较旧设备有显著提高,否则不认为有显著提高\().\)
题型:解答题 题类:历年真题 难易度:较易
新年份:2021
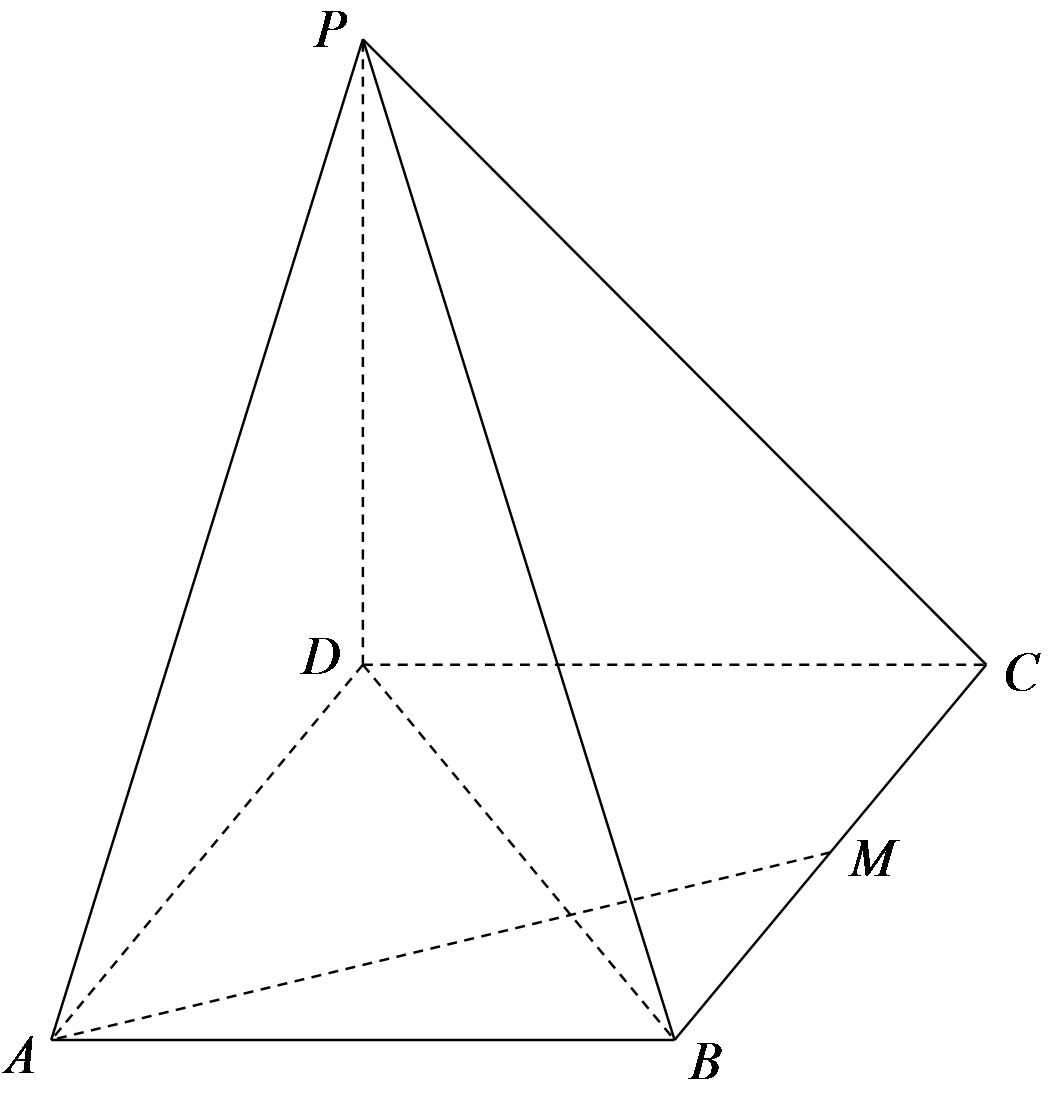
如图,四棱锥\(P-\text{ABCD}\)的底面是矩形,\(\text{PD}\text{⊥}\)底面\(\text{ABCD}\text{,}M\)为\(\text{BC}\)的中点,且\(\text{PB}\text{⊥}\text{AM}\text{.}\)
\((1)\)证明:平面\(\text{PAM}\text{⊥}\)平面\(\text{PBD}\);
\((2)\)若\(\text{PD}\text{=}\text{DC}\text{=}1\),求四棱锥\(P-\text{ABCD}\)的体积.
题型:解答题 题类:历年真题 难易度:较易
新年份:2021
设\(\left\{ a_{n}\right\}\)是首项为\(1\)的等比数列,数列\(\left\{ b_{n}\right\}\)满足\(b_{n}\text{=}\dfrac{na_{n}}{3}\text{.}\)已知\(a_{1}\text{,}3a_{2}\text{,}9a_{3}\)成等差数列.
\((1)\)求\(\left\{ a_{n}\right\}\)和\(\left\{ b_{n}\right\}\)的通项公式;
\((2)\)记\(S_{n}\)和\(T_{n}\)分别为\(\left\{ a_{n}\right\}\)和\(\left\{ b_{n}\right\}\)的前\(n\)项和.证明:\(T_{n}\text{ < }\dfrac{S_{n}}{2}.\)
题型:解答题 题类:历年真题 难易度:较易
新年份:2021
已知数列\(\left\{{{a}_{n}}\right\}\)满足\({{a}_{1}}=1\),\({a}_{n+1}{\rm=}\left\{\begin{array}{l}{a}_{n}+1,n{\rm 为奇数}\\ {a}_{n}+2,n为偶数\end{array}\right.\),
\(\left(\text{1}\right)\)记\({{b}_{n}}={{a}_{2n}}\),写出\({{b}_{1}}\),\({{b}_{2}}\),并求数列\(\left\{{{b}_{n}}\right\}\)的通项公式;
\(\left(\text{2}\right)\)求\(\left\{{{a}_{n}}\right\}\)的前\(20\)项和.
题型:解答题 题类:历年真题 难易度:较易
新年份:2021
某学校组织“一带一路”知识竞赛,有\(A\),\(B\)两类问题.每位参加比赛的同学先在两类问题中选择一类并从中随机抽取一个问题回答,若回答错误则该同学比赛结束;若回答正确则从另一类问题中再随机抽取一个问题回答,无论回答正确与否,该同学比赛结束.\(A\)类问题中的每个问题回答正确得\(20\)分,否则得\(0\)分;\(B\)类问题中的每个问题回答正确得\(80\)分,否则得\(0\)分。
已知小明能正确回答\(A\)类问题的概率为\(0.8\),能正确回答\(B\)类问题的概率为\(0.6\),且能正确回答问题的概率与回答次序无关.
\((1)\)若小明先回答\(A\)类问题,记\(X\)为小明的累计得分,求\(X\)的分布列;
\((2)\)为使累计得分的期望最大,小明应选择先回答哪类问题?并说明理由.
题型:解答题 题类:历年真题 难易度:较易
新年份:2021
在平面直角坐标系\(xOy\)中,已知点\({{F}_{1}}(-\sqrt{17},0)\),\({{F}_{2}}(\sqrt{17},0)\),点\(M\)满足\(|M{{F}_{1}}|-|M{{F}_{2}}|=2.\)记\(M\)的轨迹为\(C.\)
\((1)\)求\(C\)的方程;
\((2)\)设点\(T\)在直线\(x=\dfrac{1}{2}\)上,过\(T\)的两条直线分别交\(C\)于\(A\),\(B\)两点和\(P\),\(Q\)两点,且\(|TA|\cdot|TB|=|TP|\cdot|TQ|\),求直线\(AB\)的斜率与直线\(PQ\)的斜率之和.