选择知识点

去年\(5\)月，中央开始鼓励“地摊经济”，随即地摊在全国遍地开花。某地政府组织调研本地地摊经济，随机选取\(100\)名摊主了解他们每月的收入情况，并按收入\((\)单位：千元\()\)将摊主分成六个组\([10,15),[15,20),[20,25)[25,30),[30,35),[35,40)\)得到如下频率分布直方图：

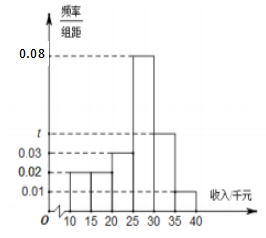
\((1)\)求频率分布直方图中\(t\)的值，并估计每月每名摊主收入的中位数和平均数\((\)单位：千元\()\)；

\((2)\)已知从收入在\(\left[15,25\right)\)的摊主中用分层抽样抽取\(5\)人，现从这\(5\)人中随机抽取\(2\)人，求抽出的\(2\) 人收入都来自\(\left[20,25\right)\)的概率。

\((Ⅰ)\)求椭圆\(M\)的方程；

\((Ⅱ)\)设直线\(l\)：\(x=ky+m\)与椭圆\(M\)交手\(A\)，\(B\)两点，若以\(AB\)为直径的圆经过椭圆的右顶点\(C\)，求\(m\)的值．

\((1)\)证明：\(BE⊥DC\)；

\((2)\)求直线\(BE\)与平面\(PBD\)所成角的正弦值；

\((3)\)若\(F\)为棱\(PC\)上一点，满足\(BF⊥AC\)，求二面角\(F-AB-P\)的余弦值．

给出问题：\(F_{1}\)，\(F_{2}\)是双曲线\(\dfrac{{{x}^{2}}}{16}-\dfrac{{{y}^{2}}}{20}=1\)的左、右焦点，点\(P\)在双曲线上．若点\(P\)到焦点\(F_{1}\)的距离等于\(9\)，求点\(P\)到焦点\(F_{2}\)的距离．某学生的解答如下：双曲线的实轴长为\(8\)，由\(||PF_{1}|-|PF_{2}||=8\)，即\(|9-|PF_{2}||=8\)，得\(|PF_{2}|=1\)或\(17.\)

该学生的解答是否正确？若正确，请写出解题依据；若不正确，请写出正确结果．

\((1)\)已知双曲线中心在原点，该双曲线过点\((4,\sqrt{3})\)，且渐近线方程为\(y=\pm\dfrac{1}{2}x\)，求该双曲线的方程.

\((2)\)已知动圆\(M\)与圆\({{C}_{1}}:{{x}^{2}}+{{y}^{2}}+6x+5=0\)外切，同时与圆\({{C}_{2}}:{{x}^{2}}+{{y}^{2}}-6x-91=0\)内切，求动圆\(M\)圆心的轨迹方程.

为了庆祝建党一百周年，某班准备举行一场小型晚会，晚会有三个歌唱节目和两个舞蹈节目，要求排出一个节目单\(.(\)用数字作答\()\)

\((1)\)两个舞蹈节目要排在一起，有多少种排法？

\((2)\)前\(3\)个节目中要有舞蹈节目，有多少种排法？

\((3)\)歌唱节目\(A\)不排在第一个，舞蹈节目\(B\)不排在最后一个，有多少种排法？

已知函数\(f(x)\)是定义在\(R\)上的奇函数，且当\(x< 0\)时，\(f(x)=-x^{2}-2x.\)

\((1)\)求函数\(f(x)(x\in\)\(R\)\()\)的解析式；

\((2)\)写出函数\(f(x)(x\in\)\(R\)\()\)的增区间\((\)不需要证明\()\)；

\((3)\)若函数\(g(x)=f(x)-2ax+2(x\in[1,2])\)，求函数\(g(x)\)的最小值．

已知圆\(C_{1}\)：\(x^{2}+y^{2}-4x-6y+12=0.\)

\((1)\)过点\(P(3,5)\)作圆\(C_{1}\)的切线\(l\)，求\(l\)的方程；

\((2)\)若圆\(C_{2}\)：\(x^{2}+y^{2}+2x-4y-4=0\)与圆\(C_{1}\)相交于\(A\)，\(B\)两点，求\(|AB|.\)

在平面直角坐标系\(xOy\)中， 点\(P\)到两点\(\left(0,-\sqrt{3}\right)\)、\(\left(0,\sqrt{3}\right)\)的距离之和等于\(4\)，设点\(P\)的轨迹为\(C\)， 直线\(y=kx+1\)与曲线\(C\)交于\(A\)、\(B\)两点\(.\:\:\: \)

\((1) \)写出曲线\(C\)的方程\(;\)

\((2) \)若\(\overrightarrow{OA}{\rm⊥}\overrightarrow{OB}\)，求\(k\)的值\(; \)

记数列\(\left\{{{a}_{n}}\right\}\)的前\(n\)项和为\({{S}_{n}}\)，在①\({{a}_{1}}=-7\)，\({{a}_{2}}=-6\)，\({a}_{n+1}=k{a}_{n}+1(n\in{\boldsymbol{\rm N}}_{+},k\in\boldsymbol{\rm R})\)；②若\(\left\{{{a}_{n}}\right\}\)为等差数列，且\({{a}_{3}}=-5\)，\({{S}_{6}}=2{{S}_{3}}+9\)；③\({S}_{n}=\dfrac{1}{2}{n}^{2}-\dfrac{15}{2}n(n\in{\boldsymbol{\rm N}}_{+}).\)这三个条件中任选一个，补充在下面问题中，并作答.

在数列\(\left\{\begin{array}{l}a_{n}\end{array}\right\}\)中，______\(.\)记\({T}_{n}=|{a}_{1}|+|{a}_{2}|+|{a}_{3}|+⋯+|{a}_{n}|\)，求\(T_{20}.\)