代数-数学-知识点同步搜题

选择知识点

题型：

全部选择题填空题解答题

难易程度：

全部易较易中档较难难

题类筛选：

全部历年真题模拟题期末考试期中考试月考试卷单元测试其他

年份：

全部 2022 2021 2020 2019 2018 2017 更早

总题量：48选择本页全部试题

题型：解答题题类：其他难易度：难
新
年份：2020

已知数列\(\{a _{n} \}\)中的相邻两项\(a _{2k-1}\)、\(a _{2k}\)是关于\(x\)的方程\(x ^{2} -(3k+2 ^{k} )x+3k\boldsymbol{⋅}2 ^{k} =0\)的两个根，且\(a _{2k-1} \leqslant a _{2k} (k=1 , 2 , 3 , …)\)．
\((\)Ⅰ\()\)求\(a _{1}\)，\(a _{3}\)，\(a _{5}\)，\(a _{7}\)及\(a _{2n} (n\geqslant 4)(\)不必证明\()\)；
\((\)Ⅱ\()\)求数列\(\{a _{n} \}\)的前\(2n\)项和\(S _{2n}\)．

查看解析收藏纠错

+选题
题型：解答题题类：其他难易度：难
新
年份：2020

如图，已知\(ABCD-A _{1} B _{1} C _{1} D _{1}\)是棱长为\(a\)的正方体，\(E\)、\(F\)分别为棱\(AA _{1}\)与\(CC _{1}\)的中点，求四棱锥的\(A _{1} -EBFD _{1}\)的体积．

查看解析收藏纠错

+选题
题型：解答题题类：其他难易度：难
新
年份：2020

是否存在实数\(p\)，使\(4x+p < 0\)是\(x ^{2} -x-2 > 0\)的充分条件？如果存在，求出\(p\)的取值范围；否则，说明理由．

查看解析收藏纠错

+选题
题型：解答题题类：其他难易度：难
新
年份：2020

设函数\(f(x)\)在\(R\)上是偶函数，在区间\((-∞ , 0)\)上递增，且\(f(2a ^{2} +a+1) < f(2a ^{2} -2a+3)\)，求\(a\)的取值范围．

查看解析收藏纠错

+选题
题型：解答题题类：其他难易度：难
新
年份：2020

倒圆锥形容器的轴截面是正三角形，内盛水的深度为\(6cm\)，水面距离容器口距离为\(1cm\)，现放入一个棱长为\(4cm\)的正方体实心铁块，让正方体一个面与水平面平行，问容器中的水是否会溢出？

查看解析收藏纠错

+选题
题型：解答题题类：其他难易度：难
新
年份：2020

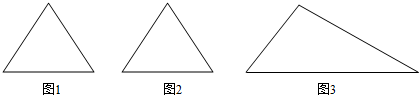
\((1)\)给出两块相同的正三角形纸片\((\)如图\(1\)，图\(2)\)，要求用其中一块剪拼成一个三棱锥模型，另一块剪拼成一个正三棱柱模型，使它们的全面积都与原三角形的面积相等，请设计一种剪拼方法，分别用虚线标示在图\(1\)、图\(2\)中，并作简要说明；
\((2)\)试比较你剪拼的正三棱锥与正三棱柱的体积的大小；
\((3)\)如果给出的是一块任意三角形的纸片\((\)如图\(3)\)，要求剪拼成一个直三棱柱，使它的全面积与给出的三角形的面积相等．请设计一种剪拼方法，用虚线标示在图\(3\)中，并作简要说明．

查看解析收藏纠错

+选题
题型：解答题题类：其他难易度：难
新
年份：2020

设函数\(f(x)= \dfrac {1-a^{x}}{1+a^{x}} (a > 0\)且\(a\neq 1)\)．
\((\)Ⅰ\()\)求函数\(f(x)\)的定义域，并判断它的奇偶性；
\((\)Ⅱ\()\)若\(f(x)\geqslant \dfrac {1}{2}\)，求\(x\)的取值范围．

查看解析收藏纠错

+选题
题型：解答题题类：其他难易度：难
新
年份：2020

已知数列\(\{a _{n} \}\)的首项\(a_{1}= \dfrac {2}{3}\)，\(a_{n+1}= \dfrac {2a_{n}}{a_{n}+1},n=1,2,3…\)．
\((1)\)证明：数列\(\{ \dfrac {1}{a_{n}}-1\}\)是等比数列；
\((2)\)求数列\(\{ \dfrac {n}{a_{n}}\}\)的前\(n\)项和为\(S _{n}\)．

查看解析收藏纠错

+选题
题型：解答题题类：其他难易度：难
新
年份：2020

已知\(f(x)= \sqrt {x^{2}-1}\)，试判断\(f(x)\)在\([1 , +∞)\)上的单调性，并证明．

查看解析收藏纠错

+选题
题型：解答题题类：其他难易度：难
新
年份：2020

已知各项均为正数的等比数列{a_n}满足a₃²=a₆，2a₃=a₅-a₄，等差数列{b_n}的前n项和为S_n，b₁=1，=λb_n+1，n∈N^*．
（1）求数列{a_n}和{b_n}的通项公式；
（2）若c_n=，且不等式t²+（1-c_n）t-c_n≤0对任意的n∈N^*恒成立，
①求c_n；
②求实数t的取值范围．

查看解析收藏纠错

+选题

高中

选择知识点

服务介绍

帮助中心