选择知识点

题型：

全部选择题填空题解答题

难易程度：

全部易较易中档较难难

题类筛选：

全部历年真题模拟题期末考试期中考试月考试卷单元测试其他

年份：

全部 2022 2021 2020 2019 2018 2017 更早

总题量：155选择本页全部试题

题型：解答题题类：历年真题难易度：较难
新
年份：2020

如图，在三棱柱ABC-A₁B₁C₁中，已知△ABC是直角三角形，侧面ABB₁A₁是矩形，AB=BC=1，BB₁=2，．
（1）证明：BC₁⊥AC．
（2）E是棱CC₁的中点，求直线B₁C与平面ABE所成角的正弦值．

查看解析收藏纠错

+选题
题型：解答题题类：历年真题难易度：较难
新
年份：2020

已知椭圆C：的离心率为，设直线l过椭圆C的上顶点和右焦点，坐标原点O到直线l的距离为2．
（1）求椭圆C的方程．
（2）过点P（8，0）且斜率不为零的直线交椭圆C于M，N两点，在x轴的正半轴上是否存在定点Q，使得直线MQ，NQ的斜率之积为非零的常数？若存在，求出定点Q的坐标；若不存在，请说明理由．

查看解析收藏纠错

+选题
题型：解答题题类：历年真题难易度：较难
新
年份：2020

在平面直角坐标系中，已知点M（-2，0），N（2，0），动点P（x，y）满足直线MP与直线NP的斜率之积为．记动点P的轨迹为曲线C．
（1）求曲线C的方程，并说明C是什么曲线；
（2）过点（，0）作直线l与曲线C交于不同的两点A，B，试问在x轴上是否存在定点Q，使得直线QA与直线QB恰好关于x轴对称？若存在，求出点Q的坐标；若不存在，请说明理由．

查看解析收藏纠错

+选题
题型：解答题题类：历年真题难易度：较难
新
年份：2020

在平面直角坐标系xOy中，点B与点A（-1，1）关于原点对称，P是动点，且直线AP与BP的斜率之积等于．
（1）求动点P的轨迹方程，并注明x的范围；
（2）设直线AP与BP分别与直线x=3交于M，N，问是否存在点P使得△PAB与△PMN面积相等？若存在，求出点P的坐标，若不存在，说明理由．

查看解析收藏纠错

+选题
题型：解答题题类：历年真题难易度：较难
新
年份：2020

如图，四棱锥P-ABCD中，四边形ABCD是边长为4的菱形，PA=PC，BD⊥PA，E是BC上一点，且BE=1，设AC∩BD=O．
（1）证明：PO⊥平面ABCD；
（2）若∠BAD=60°，PA⊥PE，求三棱锥P-AOE的体积．

查看解析收藏纠错

+选题
题型：解答题题类：历年真题难易度：较难
新
年份：2020

已知抛物线C：y²=2px（p＞0）与直线l：x+y+1=0相切于点A，点B与A关于x轴对称．
（1）求抛物线C的方程，及点B的坐标；
（2）设M、N是x轴上两个不同的动点，且满足∠BMN=∠BNM，直线BM、BN与抛物线C的另一个交点分别为P、Q，试判断直线PQ与直线l的位置关系，并说明理由．如果相交，求出的交点的坐标．

查看解析收藏纠错

+选题
题型：解答题题类：历年真题难易度：较难
新
年份：2020

为筛查在人群中传染的某种病毒，现有两种检测方法：
（1）抗体检测法：每个个体独立检测，每一次检测成本为80元，每个个体收取检测费为100元．
（2）核酸检测法：先合并个体，其操作方法是：当个体不超过10个时，把所有个体合并在一起进行检测．
当个体超过10个时，每10个个体为一组进行检测．若该组检测结果为阴性（正常），则只需检测一次；若该组检测结果为阳性（不正常），则需再对每个个体按核酸检测法重新独立检测，共需检测k+1次（k为该组个体数，1≤k≤10，k∈N^*）．每一次检测成本为160元．假设在接受检测的个体中，每个个体的检测结果是阳性还是阴性相互独立，且每个个体是阳性结果的概率均为p（0＜p＜1）．
（Ⅰ）现有100个个体采取抗体检测法，求其中恰有一个检测出为阳性的概率；
（Ⅱ）因大多数人群筛查出现阳性的概率很低，且政府就核酸检测法给子检测机构一定的补贴，故检测机构推出组团选择核酸检测优惠政策如下：无论是检测一次还是k+1次，每组所有个体共收费700元（少于10个个体的组收费金额不变）．已知某企业现有员工107人，准备进行全员检测，拟准备9000元检测费，由于时间和设备条件的限制，采用核酸检测法合并个体的组数不得高于参加采用抗体检测法人数，请设计一个合理的的检测安排方案；
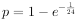（Ⅲ）设，现有n（n∈N^*且2≤n≤10）个个体，若出于成本考虑，仅采用一种检测方法，试问检测机构应采用哪种检测方法？（ln3≈1.099，ln4≈1.386，ln5≈1.609，ln6≈1.792）

查看解析收藏纠错

+选题
题型：解答题题类：历年真题难易度：较难
新
年份：2020

（1）证明：；
（2）证明：对一切正整数n和一切实数x（x≠0，-1，…，-n），有．

查看解析收藏纠错

+选题
题型：解答题题类：历年真题难易度：较难
新
年份：2020

某药业公司统计了2010-2019年这10年某种疾病的患者人数，结论如下：该疾病全国每年的患者人数都不低于100万，其中有3年的患者人数低于200万，有6年的患者人数不低于200万且低于300万，有1年的患者人数不低于300万．
（1）药业公司为了解一新药品对该疾病的疗效，选择了200名患者，随机平均分为两组作为实验组和对照组，实验结束时，有显著疗效的共110人，实验组中有显著疗效的比率为70%．请完成如下的2×2列联表，并根据列联表判断是否有99.9%把握认为该药品对该疾病有显著疗效；

实验组对照组合计

有显著疗效

无显著疗效

合计 200

（2）药业公司最多能引进3条新药品的生产线，据测算，公司按如下条件运行生产线：

该疾病患者人数（单位：万） 100≤x＜200 200≤x＜300 X≥300

最多可运行生产线数 1 2 3

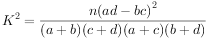每运行一条生产线，可产生年利润6000万元，没运行的生产线毎条每年要亏损1000万元．根据该药业公司这10年的统计数据，将患者人数在以上三段的频率视为相应段的概率、假设各年的患者人数相互独立．欲使该药业公司年总利润的期望值达到最大，应引进多少条生产线？
附：参考公式：，其中n=a+b+c+d．

P（K²≥k₀） 0.05 0.025 0.010 0.001

k₀ 3.841 5.024 6.635 10.828

查看解析收藏纠错

+选题
题型：解答题题类：历年真题难易度：较难
新
年份：2020

已知椭圆Γ：的焦点F₁，F₂的距离为，过F₂且垂直于x轴的直线交椭圆Γ于A，B两点，且|AB|=1．
（Ⅰ）求椭圆Γ的方程；
（Ⅱ）若存在实数t，使得经过相异两点P（4t，t²+h）和Q（2t+2，t+h）的直线交椭圆Γ所得弦的中点恰为点Q，求实数h的取值范围．

查看解析收藏纠错

+选题