4.3.1 直线与平面平行-山东版高教版（拓展上）数学同步练习题

题型：

全部选择题填空题解答题

难易程度：

全部易较易中档较难难

题类筛选：

全部历年真题模拟题期末考试期中考试月考试卷单元测试其他

年份：

全部 2022 2021 2020 2019 2018 2017 更早

总题量：26 选择本页全部试题

题型：解答题题类：历年真题难易度：较易

年份：2018

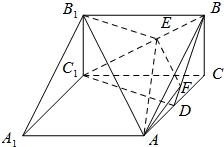如图，三棱柱\(ABC-A_{1}B_{1}C_{1}\)中，\(BC\)垂直于正方形\(A_{1}ACC_{1}\)所在平面，\(AC=2\)，\(BC=1\)，\(D\)为\(AC\)中点，\(E\)为线段\(BC_{1}\)上的一点\((\)端点除外\()\)，平面\(AB_{1}E\)与\(BD\)交于点\(F\)
\((\)Ⅰ\()\)若\(E\)不是\(BC_{1}\)的中点，求证：\(AB_{1}/\!/EF\)；
\((\)Ⅱ\()\)若\(E\)是\(BC_{1}\)的中点，求\(AE\)与平面\(BC_{1}D\)所成角的正弦值；
\((\)Ⅲ\()\)在线段\(BC_{1}\)上是否存在点\(E\)，使得\(A_{1}E⊥CE\)，若存在，求出\( \dfrac {BE}{EC_{1}}\)的值，若不存在，请说明理由．

查看解析收藏纠错相似题

+选题
题型：选择题题类：历年真题难易度：较易
测
年份：2018

在空间四边形\(ABCD\)中，\(E\)，\(F\)分别为\(AB\)，\(AD\)上的点，且\(AE\)：\(EB=AF\)：\(FD=1\)：\(4\)，又\(H\)，\(G\)分别是\(BC\)，\(CD\)的中点，则\((\)　　\()\)

A.\(BD/\!/\)平面\(EFG\)，且四边形\(EFGH\)是平行四边形 B.\(EF/\!/\)平面\(BCD\)，且四边形\(EFGH\)是梯形 C.\(HG/\!/\)平面\(ABD\)，且四边形\(EFGH\)是平行四边形 D.\(EH/\!/\)平面\(ADC\)，且四边形\(EFGH\)是梯形

查看解析收藏纠错相似题

+选题
题型：选择题题类：历年真题难易度：较易
测
年份：2018

若平面 \(α\)\(/\!/\)平面 \(β\)，点 \(A\)， \(C\)\(∈\) \(α\)， \(B\)， \(D\)\(∈\) \(β\)，则直线 \(AC\)\(/\!/\)直线 \(BD\)的充要条件是( )

A.\(AB\)\(/\!/\) \(CD\) B.\(AD\)\(/\!/\) \(CB\) C.\(AB\)与 \(CD\)相交 D.\(A\)， \(B\)， \(C\)， \(D\)四点共面

查看解析收藏纠错相似题

+选题
题型：选择题题类：历年真题难易度：较易
测
年份：2018

已知\(m\)，\(n\)是两条不同直线，\(α\)，\(β\)，\(γ\)是三个不同平面，下列命题中正确的是 \((\)   \()\)


A.若\(m/\!/α\)，\(n/\!/α\)，则\(m/\!/n\)    B.若\(α⊥γ\)，\(β⊥γ\)，则\(α/\!/β\)

C.若\(m/\!/α\)，\(m/\!/β\)，则\(α/\!/β\)    D.若\(m⊥α\)，\(n⊥α\)，则\(m/\!/n\)

查看解析收藏纠错相似题

+选题
题型：填空题题类：历年真题难易度：较易

年份：2018

已知\(a\)，\(b\)为两条不同的直线，\(α\)，\(β\)，\(γ\)为三个不同的平面，给出以下三个说法：

\(①\)若\(a/\!/b\)，\(b⊂α\)，则\(a/\!/α;\)

\(②\)若\(a/\!/b\)，\(a/\!/α\)，则\(b/\!/α;\)

\(③\)若\(α∩β=a\)，\(b⊂γ\)，且\(b/\!/β\)，\(a⊂γ\)，则\(a/\!/b\)．

其中正确说法的序号是____\(.\)

查看解析收藏纠错相似题

+选题
题型：解答题题类：历年真题难易度：较易

年份：2018

如图，四棱柱\(ABCD-A_{1}B_{1}C_{1}D_{1}\)的底面\(ABCD\)是菱形，\(AC\cap BD=0\)，\(A_{1}O⊥\)底面\(ABCD\)，\(AB=2\)，\(AA_{1}=3\)．

\((1)\)证明：平面\(A_{1}CO⊥\)平面\(BB_{1}D_{1}D\)；

\((2)\)若\(∠BAD=60^{\circ}\)，求二面角\(B-OB_{1}-C\)的余弦值．

查看解析收藏纠错相似题

+选题
题型：选择题题类：历年真题难易度：较易
测
年份：2018

有下列四个说法：

\(①\)若直线\(l\)平行于平面\(α\)内的无数条直线，则直线\(l/\!/α;\)

\(②\)若直线\(a\)在平面\(α\)外，则\(a/\!/α;\)

\(③\)若直线\(a/\!/b\)，\(b/\!/α\)，则\(a/\!/α;\)

\(④\)若直线\(a/\!/b\)，\(b/\!/α\)，则\(a\)平行于平面\(α\)内的无数条直线．

其中正确说法的个数是 \((\)　　\()\)

A.\(1\) B.\(2\) C.\(3\) D.\(4\)

查看解析收藏纠错相似题

+选题
题型：选择题题类：历年真题难易度：较易
测
年份：2018

已知\(m\)和\(n\)是两条不同的直线，\(α\)和\(β\)是两个不重合的平面，下面给出的条件中一定能推出\(m⊥β\)的是 ( )

A.\(α⊥β\)且\(m⊂α\) B.\(α⊥β\)且\(m/\!/α\) C.\(m/\!/n\)且\(n⊥β\) D.\(m⊥n\)且\(α/\!/β\)

查看解析收藏纠错相似题

+选题
题型：填空题题类：历年真题难易度：较易

年份：2018

已知\(a\)，\(b\)，\(l\)表示三条不同的直线，\(α\)，\(β\)，\(γ\)表示三个不同的平面，有下列四个说法：

\(①\)若\(α∩β=a\)，\(β∩γ=b\)，且\(a/\!/b\)，则\(α/\!/γ;\)

\(②\)若\(a\)，\(b\)相交，且都在\(α\)，\(β\)外，\(a/\!/α\)，\(a/\!/β\)，\(b/\!/α\)，\(b/\!/β\)，则\(α/\!/β;\)

\(③\)若\(α⊥β\)，\(α∩β=a\)，\(b⊂β\)，\(a⊥b\)，则\(b⊥α;\)

\(④\)若\(a⊂α\)，\(b⊂α\)，\(l⊥a\)，\(l⊥b\)，\(l⊄α\)，则\(l⊥α\)．

其中正确说法的序号是____\(.\)

查看解析收藏纠错相似题

+选题
题型：选择题题类：历年真题难易度：较易
测
年份：2018

已知平面\(α\)、\(β\)和直线 \(a\)、\(b\)，下列说法正确的是\((\)　　\()\)

A.若 \(a\:/\!/α\)，\(b\:/\!/β\)，则 \(a\:/\!/b\) B.若 \(a⊂α\)，\(b⊂β\)，且 \(a\:/\!/b\)，则\(α\:/\!/β\) C.若 \(a⊥α\)，\(b⊥β\)，且 \(a\:/\!/b\)，则\(α\:/\!/β\) D.若\(α⊥β\)，\(a⊂α\)，\(b⊂β\)，则 \(a⊥b\)

查看解析收藏纠错相似题

+选题

1 2 3 下一页共3页跳转

高中

选择章节

服务介绍

帮助中心