题型:解答题 题类:单元测试 难易度:较易
新年份:2021
如图\(1\),在\(\triangle MBC\)中,\(BM⊥BC\),\(A\),\(D\)分别为边\(MB\),\(MC\)的中点,且\(BC=AM=2\),将\(\triangle MAD\)沿\(AD\)折起到\(\triangle PAD\)的位置,使\(PA⊥AB\),如图\(2\),连接\(PB\),\(PC.\)
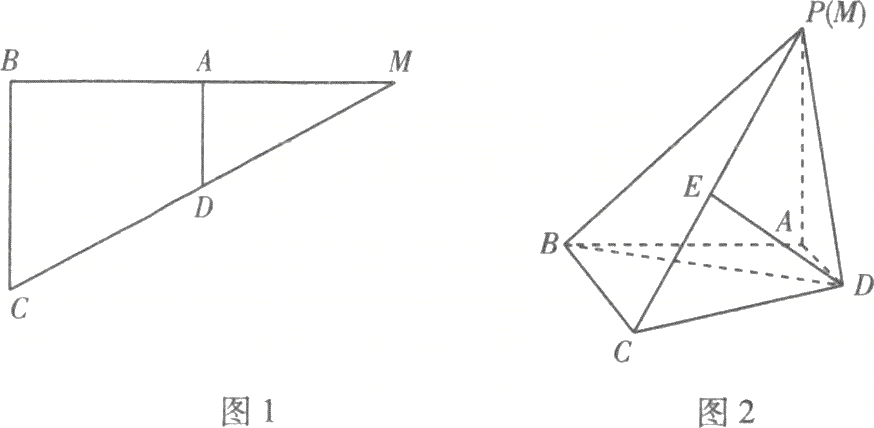
\((1)\)求证:\(PA⊥\)平面\(ABCD\):
\((2)\)若\(E\)为\(PC\)的中点,求直线\(DE\)与平面\(PBD\)所成角的正弦值;
\((3)\)线段\(PC\)上一动点\(G\)满足\(\dfrac{PG}{PC}=\lambda(0\leqslant λ\leqslant 1)\),判断是否存在\(λ\),使二面角\(G-AD-P\)的正弦值为\(\dfrac{\sqrt{10}}{10}\),若存在,求出\(λ\)的值;若不存在,请说明理由.