题型:选择题 题类:期中考试 难易度:较难
测年份:2018
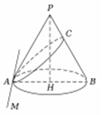
\(2000\)多年前,古希腊大数学家阿波罗尼奥斯\((Apollonius)\)发现:平面截圆锥的截口曲线是圆锥曲线\(.\)已知圆锥的高为\(PH\),\(AB\)为底面直径,顶角为\(2\theta \),那么不过顶点\(P\)的平面:与\(PH\)夹角\(\alpha \)满足\(\dfrac{\pi }{2} > \alpha > \theta \)时,截口曲线为椭圆;与\(PH\)夹角\(\alpha =\theta \)时,截口曲线为抛物线;与\(PH\)夹角\(\alpha \)满足\(\theta > \alpha > 0\)时,截口曲线为双曲线\(.\)如图,底面内的直线\(AM\bot AB\),过\(AM\)的平面截圆锥得到的曲线为椭圆,其中与\(PB\)的交点为\(C\),可知\(AC\)为长轴\(.\)那么当\(C\)在线段\(PB\)上运动时,截口曲线的短轴顶点的轨迹为\((\) \()\)