选择章节

如图，在四棱锥\(P-ABCD\)中，\(PA\bot\)平面\(ABCD\)，\(PA=AB=BC=2\)，\(AD=CD\)，\(\angle ABC=120{}^\circ.\)

\((1)\)求证：平面\(PAC\bot\)平面\(PBD\)；

\((2)\)若点\(M\)为\(PB\)的中点，点\(N\)为线段\(PC\)上一动点，求直线\(MN\)与平面\(PAC\)所成角的正弦值的取值范围.

在三棱柱\(ABC-AB{{C}_{1}}\)中，侧面\(AC{{C}_{1}}{{A}_{1}}\)是正方形，\(A{{A}_{1}}=A{{B}_{1}}={{B}_{1}}C=2\)，\(AB=BC\)，\(AB\bot BC.\)

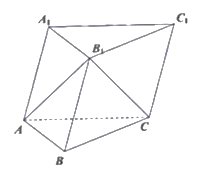
\((1)\)求证：平面\(A{{B}_{1}}C\bot\)平面\(ABC\)；

\((2)\)线段\({{B}_{1}}C\)上是否存在点\(E\)，使得直线\({{A}_{1}}E\)与平面\(A{{B}_{1}}C\)所成角为\(\dfrac{\pi}{6}\)？

如图，已知四棱锥\({\rm P}-ABCD\)的底面\(ABCD\)为菱形，\(PA{\rm⊥}\)平面\(ABCD\)，\({\rm∠}ABC={60}^{∘}\)，\(E,F\)分别是\(BC,PC\)的中点．

\((1)\)证明：\(AE{\rm⊥}PD\)；

\((2)\)若\(H\)为\(PD\)上的动点，\(EH\)与平面\(PAD\)所成最大角的正切值为\(\dfrac{\sqrt{6}}{2}\)，求二面角\({\rm E}-AF-{\rm C}\)的余弦值．

如图，在四棱锥\(P-ABCD\)中，\(PA\bot\)底面\(ABCD\)，\(AD\bot AB\)，\(DC\text{//}AB\)，\(PA=AD=DC=1\)，\(AB=2\)，\(E\)为棱\(PB\)上一点.

\((1)\)若\(E\)为棱\(PB\)的中点，求证：直线\(CE\text{//}\)平面\(PAD\)；

\((2)\)若\(E\)为棱\(PB\)上存在异于\(P､B\)的一点，且二面角\(E-AC-B\)的平面角的余弦值为\(\dfrac{\sqrt{6}}{3}\)，求直线\(AE\)与平面\(ABCD\)所成角的正弦值.

四棱锥\(S-ABCD\)的底面\(ABCD\)为直角梯形，\(AB=2BC=2CD=4\)，\(AB⊥BC\)，\(AB\://\:CD\)，\(SA=SD\)，且平面\(SAD⊥\)平面\(ABCD\)，\(M\)为\(AB\)中点．

\((1)\)求证：\(CM⊥SM\)；

\((2)\)若直线\(SB\)与平面\(SAD\)所成的角为\(\dfrac{\pi}{4}\)，求平面\(SAD\)与平面\(SBC\)的夹角的余弦值．

如图，在四棱锥\(P-ABCD\)中，底面\(ABCD\)是矩形，\(PA\bot AB\)，\(AB=2BC=2\)，\(PC=3\)，\(PA=2\)，\(E\)为\(PD\)的中点.

\((1)\)证明：\(BC\bot\)平面\(PAB\)；

\((2)\)求直线\(EB\)与平面\(PBC\)所成角的正弦值.