(2022•山东)(本小题8分)如图所示,已知等边\( \mathrm{\angle }\mathrm{A}\mathrm{B}\mathrm{C}\)的边长为6,顺次连接\( △\mathrm{A}\mathrm{B}\mathrm{C}\)各边的中点,构成\( \mathrm{\angle }{\mathrm{A}}_{1}{\mathrm{B}}_{1}{\mathrm{C}}_{1}\),再顺次连接\( \mathrm{\angle }{\mathrm{A}}_{1}{\mathrm{B}}_{1}{\mathrm{C}}_{1}\)各边的中点,构成\( \mathrm{\angle }{\mathrm{A}}_{2}{\mathrm{B}}_{2}{\mathrm{C}}_{2}\),依此进行下去,直至构成\( \mathrm{\angle }{\mathrm{A}}_{\mathrm{n}}{\mathrm{B}}_{\mathrm{n}}{\mathrm{C}}_{\mathrm{n}}\),这n个新构成的三角形的边长依次记作\( {\mathrm{\alpha }}_{1}\),\( {\mathrm{\alpha }}_{2}\),…,\( {\mathrm{\alpha }}_{\mathrm{n}}.\)
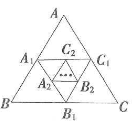
(1)求\( {\mathrm{\alpha }}_{1}\),\( {\mathrm{\alpha }}_{2}\),\( {\mathrm{\alpha }}_{3}\)的值;
(2)若\( \mathrm{\angle }{\mathrm{A}}_{\mathrm{n}}{\mathrm{B}}_{\mathrm{n}}{\mathrm{C}}_{\mathrm{n}}\)的边长小于0.01,求n的最小值
.
,求实数
的取值范围；
的定义域为R，求m的取值范围。 
满足：\( a₃=7,a₃+a₇=26,a\mathrm{ₙ}\)的前n项和为S。.
为等比数列. 
