题型:填空题 题类:模拟题 难易度:较难
年份:2018
\((1)\)设\(\alpha \)为锐角, 若\(\cos \left( \alpha +\dfrac{\pi }{6} \right)=\dfrac{4}{5}\),则\(\sin \alpha \)的值为_________.
\((2)\)在边长为\(2\)的正三角形\(ABC\)中,设\(\overrightarrow{BC}=2 \overrightarrow{BD}, \overrightarrow{CA}=3 \overrightarrow{CE} \),则\(\overrightarrow{AD}\cdot \overrightarrow{BE}=\)_____________.
\((3)\)已知正四面体\(ABCD\)中,\(E\)是\(AB\)的中点,则异面直线\(CE\)与\(BD\)所成角的余弦值为__________.
\((4)\)若\(f\left( x \right)=A{\sin }\left( \omega +\varphi \right)+3(\omega > 0,\left| \varphi \right| < { }\!\!\pi\!\!{ })\)对任意实数\(t\)都有\(f\left( t+\dfrac{{ }\!\!\pi\!\!{ }}{3} \right)=f\left( -t+\dfrac{{ }\!\!\pi\!\!{ }}{3} \right).\)记\(g\left( x \right)=A{\cos }\left( \omega x+\varphi \right)-2\),则\(g\left( \dfrac{{ }\!\!\pi\!\!{ }}{3} \right)=\)_______.
题型:填空题 题类:模拟题 难易度:较难
年份:2018
已知函数\(f(x)=\begin{cases} 2x{+}\cos x\mathrm{{,}}x{\geqslant }0\mathrm{{,}} \\ x\mathrm{(}a\mathrm{{-}}x\mathrm{){,}}x{ < }0\mathrm{{.}} \end{cases}\)若关于\(x\)的不等式\(f(x) < π\)的解集为\(\left( \mathrm{{-}}\mathrm{{∞}}\mathrm{{,}}\dfrac{\pi}{2} \right)\),则实数\(a\)的取值范围是____\(.\)
题型:填空题 题类:模拟题 难易度:较难
年份:2018
\((1)\)能够说明“设\(a{,}b{,}c\)是任意实数\({.}\)若\(a{ > }b{ > }c\),则\(a{+}b{ > }c\)”是假命题的一组整数\(a{,}b{,}c\)的值依次为______ .
\((2)\)直线\(l\)与椭圆\(\dfrac{x^{2}}{4}{+}y^{2}{=}1\)相交于\(A{,}B\)两点,若弦\(AB\)中点为\(({-}1{,}\dfrac{1}{2})\),则直线\(l\)的方程为______ .
\((3)\)已知数列\(\{ a_{n}\}\)和\(\{ b_{n}\}\),其中\(a_{n}{=}n^{2}{,}n{∈}N^{{*}}{,}\{ b_{n}\}\)的项是互不相等的正整数,若对于任意\(n{∈}N^{{*}}{,}\{ b_{n}\}\)的第\(a_{n}\)项等于\(\{ a_{n}\}\)的第\(b_{n}\)项,则\(\dfrac{\lg(b_{1}b_{4}b_{9}b_{16})}{\lg(b_{1}b_{2}b_{3}b_{4})}{=}\) ______ .
\((4)\)已知双曲线\(C\):\(\dfrac{x^{2}}{a^{2}}{-}\dfrac{y^{2}}{b^{2}}{=}1(a{ > }0{,}b{ > }0)\)的右顶点为\(A\),以\(A\)为圆心,\(b\)为半径作圆\(A\),圆\(A\)与双曲线\(C\)的一条渐近线交于\(M\)、\(N\)两点\({.}\)若\({∠}{MAN}{=}60^{{∘}}\),则\(C\)的离心率为______ .
题型:填空题 题类:模拟题 难易度:较难
年份:2018
\((1)\)在平面直角坐标系\(xOy\)中,双曲线\( \dfrac{x^{2}}{a^{2}}-y^{2}=1\)与抛物线\(y^{2}=-12x\)有相同的焦点,则双曲线的两条渐近线的方程为________.
\((2)\)在\(\triangle ABC\)中,\(D\)为\(BC\)边的中点,\(AD=2\),点\(P\)在线段\(AD\)上,则\(\overrightarrow{PA}·(\overrightarrow{PB}+\overrightarrow{PC})\)的最小值为________.
\((3)\)关于统计数据的分析,有以下几个结论:
\(①\)一组数可能有两个众数;
\(②\)将一组数据中的每个数据都减去同一个数后,方差没有变化;
\(③\)调查剧院中观众观看感受时,从\(50\)排\((\)每排人数相同\()\)中任意抽取一排的人进行调查,属于分层抽样;
\(④\)一组数据的方差一定是正数;
\(⑤\)如图是随机抽取的\(200\)辆汽车通过某一段公路时的时速频率分布直方图,根据这个直方图,可以得到时速在\([50,60)\)的汽车大约是\(60\)辆.

其中说法错误的有________\(.(\)填序号\()\)
\((4)\)将各位数字和为\(11\)的全体正整数按自小到大的顺序排成一个数列,则\(2018\)是该数列的第_____ 项
题型:填空题 题类:模拟题 难易度:较难
年份:2018
\((1)\)设实数\(x\),\(y\)满足不等式组\(\begin{cases}\begin{matrix}x+2y\leqslant 10 \\ 2x+y⩾3\end{matrix} \\ \begin{matrix}0\leqslant x\leqslant 4 \\ y\geqslant 1\end{matrix}\end{cases} \),则\(z=|x+y-10|\)的最大值是________.
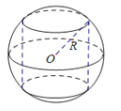
\((2)\)如图所示,半径\(R=2\)的球\(O\)中有一内接圆柱,当圆柱的侧面积最大时,球的表面积与圆柱的侧面积之差等于________
\((3)\)椭圆\( \dfrac{{x}^{2}}{{a}^{2}}+ \dfrac{{y}^{2}}{{b}^{2}}=1\left(a > b > 0\right) \)的右焦点\(F(c,0)\) 关于直线\(y= \dfrac{b}{c}x \)的对称点在椭圆上,则椭圆的离心率是________ \(.\)
\((4)\)已知\(A\),\(B\),\(C\)三人中,一个是油漆工,一个是木工,一个是泥瓦工,但不知\(A\),\(B\),\(C\)三人具体谁是什么工种,三人合作一件工程,由于其中的某一个人而做糟了,为了弄清楚责任,分别询问三人,得到的回答如下: \(A\)说:\("C\)做坏了,\(B\)做好了\("\);\(B\)说:\("\)我做坏了,\(C\)做好了\("\);\(C\)说:\("\)我做坏了,\(A\)做好了\(".\)现在又了解到,油漆工从来不说假话,泥瓦工从来不说真话,而木工说的话总是时真时假,则该负责任的是________\(.\)