代数-数学-知识点同步搜题

选择知识点

题型：

全部选择题填空题解答题

难易程度：

全部易较易中档较难难

题类筛选：

全部历年真题模拟题期末考试期中考试月考试卷单元测试其他

年份：

全部 2022 2021 2020 2019 2018 2017 更早

总题量：301选择本页全部试题

题型：解答题题类：期末考试难易度：易
新
年份：2020

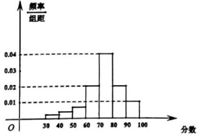某学校高二年级有\(2000\)名学生进行了一次物理测试，根据男女学生人数比例，使用分层抽样的方法从中抽取了\(100\)名学生作为样本，记录他们的成绩数据，将数据分成\(7\)组：\([30 , 40)\)，\([40 , 50)\)，\(…[90 , 100]\)，整理得到如图频率分布直方图．
\((1)\)若该样本中男生有\(60\)人，试估计该学校高二年级女生总人数；
\((2)\)根据频率分布直方图，求样本中物理成绩在\([70 , 90)\)的频率；
\((3)\)用频率估计概率，现从该校高二年级学生中随机抽取\(2\)人，求恰有一名学生的物理成绩在\([70 , 90)\)的概率．

查看解析收藏纠错

+选题
题型：解答题题类：期末考试难易度：易
新
年份：2020

\((1)\)求\((-x+ \dfrac {1}{2x} ) ^{6}\)的展开式的各项系数之和及展开式的常数项．
\((2)4\)位男同学与\(3\)位女同学任意排成一排照相．
\((i)\)求\(3\)位女同学站在一起的概率；
\((ii)\)求\(4\)位男同学互不相邻的概率．

查看解析收藏纠错

+选题
题型：解答题题类：期末考试难易度：易
新
年份：2020

化简求值：
\((1)(0.064) ^{- \frac {1}{3}} -(- \dfrac {7}{8} ) ^{0} +[(-2) ^{3} ] ^{- \frac {4}{3}} +16 ^{-0.75}\)；
\((2)2\log _{3} 2-\log _{3} \dfrac {32}{9} +\log _{3} 8-5 ^{\log _{5}3}\)．

查看解析收藏纠错

+选题
题型：解答题题类：期末考试难易度：易
新
年份：2020

设全集\(U=R\)，集合\(A=\{x|3 ^{x} \geqslant 9\}\)，\(B=\{x|a\leqslant x\leqslant a+3\}\)．
\((1)\)当\(a=1\)时，求\(A∩B\)；
\((2)\)若\(A∪B=A\)，求实数\(a\)的取值范围．

查看解析收藏纠错

+选题
题型：解答题题类：期末考试难易度：易
新
年份：2020

在\((x- \dfrac {1}{x} ) ^{9}\)展开式中，求：
\((1)\)含\(x\)的项；
\((2)\)含\(x ^{3}\)的项的系数．

查看解析收藏纠错

+选题
题型：解答题题类：期末考试难易度：易
新
年份：2020

已知\(f(x)= \dfrac {3^{x}+\;a}{3^{x}+1}\)是奇函数．
\((1)\)求实数\(a\)的值；
\((2)\)判断函数\(f(x)\)的单调性\((\)只写出判断结果，不需要证明\()\)．

查看解析收藏纠错

+选题
题型：解答题题类：期末考试难易度：易
新
年份：2020

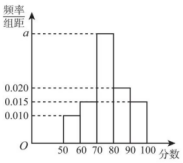有\(1000\)人参加了某次垃圾分类知识竞赛，从中随机抽取\(100\)人，将这\(100\)人的此次竞赛的分数分成\(5\)组：\([50 , 60)\)，\([60 , 70)\)，\([70 , 80)\)，\([80 , 90)\)，\([90 , 100]\)，并整理得到如下频率分布直方图．
\((\)Ⅰ\()\)求图中\(a\)的值；
\((\)Ⅱ\()\)估计总体\(1000\)人中竞赛分数不少于\(70\)分的人数；
\((\)Ⅲ\()\)假设同组中的每个数据都用该组区间的中点值代替，估计总体\(1000\)人的竞赛分数的平均数．

查看解析收藏纠错

+选题
题型：解答题题类：期末考试难易度：易
新
年份：2020

课外活动小组共\(13\)人，其中男生\(8\)人，女生\(5\)人，并且男、女生各指定一名队长，现从中选\(5\)人主持某种活动，依下列条件各有多少种选法？
\((1)\)只有\(1\)名女生当选；
\((2)\)两名队长当选；
\((3)\)至少有\(1\)名队长当选；
\((4)\)至多有\(2\)名女生当选；
\((5)\)既要有队长，又要有女生当选．

查看解析收藏纠错

+选题
题型：解答题题类：期末考试难易度：易
新
年份：2020

已知函数\(f(x)=- \sqrt {3} \cos \dfrac {1}{3}x- \sin \dfrac {1}{3}x+3\)．
\((1)\)求\(f(x)\)图象的对称轴方程；
\((2)\)求\(f(x)\)的最小值及此时自变量\(x\)的取值集合．

查看解析收藏纠错

+选题
题型：解答题题类：期末考试难易度：易
新
年份：2020

在直角\(\triangle ABC\)中，\(A= \dfrac {π}{2}\)，\(D\)为\(AC\)边上的一点，\(BD= \sqrt {3}\)．
\((1)\)若\(BC=3\)，\(∠BDC= \dfrac {2π}{3}\)，求\(\triangle BDC\)的面积；
\((2)\)若\(C= \dfrac {π}{3}\)，求\(\triangle BCD\)周长\(l\)的取值范围．

查看解析收藏纠错

+选题

高中

选择知识点

服务介绍

帮助中心