代数-数学-知识点同步搜题

选择知识点

题型：

全部选择题填空题解答题

难易程度：

全部易较易中档较难难

题类筛选：

全部历年真题模拟题期末考试期中考试月考试卷单元测试其他

年份：

全部 2022 2021 2020 2019 2018 2017 更早

总题量：60选择本页全部试题

题型：解答题题类：模拟题难易度：易
新
年份：2020

某中学举行电脑知识竞赛，现将高一参赛学生的成绩进行整理后分成五组绘制成如图所示的频率分布直方图；
\((1)\)求高一参赛学生的成绩的众数、中位数；
\((2)\)求高一参赛学生的平均成绩．

查看解析收藏纠错

+选题
题型：解答题题类：模拟题难易度：易
新
年份：2020

已知数列{a_n}的前n项和为S_n，且4S_n+5=5a_n，n∈N^*．
（Ⅰ）求数列{a_n}的通项公式；
（Ⅱ）若数列{b_n}满足：b_n=，设数列{b_n}的前n项和为T_n，证明：T_n＜1

查看解析收藏纠错

+选题
题型：解答题题类：模拟题难易度：易
新
年份：2020

已知椭圆\(C\)：\( \dfrac {x^{2}}{a^{2}}+ \dfrac {y^{2}}{b^{2}}=1 (a > b > 0)\)的长轴长为\(4\)，过焦点且垂直于\(x\)轴的直线被椭圆\(C\)截得的线段长为\(1\)．
\((1)\)求椭圆\(C\)的方程；
\((2)\)若点\(A(0 , 2)\)，点\(Q(x _{1} , y _{1} )(x _{1} y _{1} \neq 0)\)在椭圆\(C\)上，\(QM⊥x\)轴，垂足为\(M\)，直线\(AN⊥AM\)交\(x\)轴于点\(N\)，线段\(EN\)的中点为坐标原点，试判断直线\(QE\)与椭圆\(C\)的位置关系．

查看解析收藏纠错

+选题
题型：解答题题类：模拟题难易度：易
新
年份：2020

设数列{a_n}的前n项和为S_n，且S_n=λn²-16n+m．
（1）当λ=2时，求通项公式a_n；
（2）设{a_n}的各项为正，当m=15时，求λ的取值范围．

查看解析收藏纠错

+选题
题型：解答题题类：模拟题难易度：易
新
年份：2020

环保部门要对所有的新车模型进行广泛测试，以确定它的行车里程的等级，右表是对\(100\)辆新车模型在一个耗油单位内行车里程\((\)单位：公里\()\)的测试结果．

分组频数

\([30 , 32)\) \(6\)

\([32 , 34)\) \(10\)

\([34 , 36)\) \(20\)

\([36 , 38)\) \(30\)

\([38 , 40)\) \(18\)

\([40 , 42)\) \(12\)

\([42 , 44)\) \(4\)

\((\)Ⅰ\()\)做出上述测试结果的频率分布直方图，并指出其中位数落在哪一组；
\((\)Ⅱ\()\)用分层抽样的方法从行车里程在区间\([38 , 40)\)与\([40 , 42)\)的新车模型中任取\(5\)辆，并从这\(5\)辆中随机抽取\(2\)辆，求其中恰有一个新车模型行车里程在\([40 , 42)\)内的概率．

查看解析收藏纠错

+选题
题型：解答题题类：模拟题难易度：易
新
年份：2020

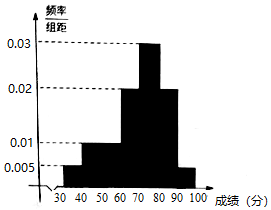为推进中小学体育评价体系改革，某调研员从一中学\(4000\)名学生中按照男女学生比例采用分层抽样的方法，从中随机抽取了\(400\)名学生进行某项体育测试\((\)满分\(100\)分\()\)，记录他们的成绩，将记录的数据分成\(7\)组：\((30 , 40]\)，\((40 , 50]\)，\((50 , 60]\)，\((60 , 70]\)，\((70 , 80]\)，\((80 , 90]\)，\((90 , 100]\)，并整理得到如图频率分布直方图．
\((\)Ⅰ\()\)根据该频率分布直方图，估计样本数据的中位数及\(4000\)名学生的平均成绩\((\)同一组中的数据用该组区间的中点值作代表\()(\)精确到\(0.01)\)；
\((\)Ⅱ\()\)已知样本中有三分之二的男生分数高于\(60\)分，且分数高于\(60\)分的男女人数相等，试估计该校男生和女生人数的比例；
\((\)Ⅲ\()\)若测试成绩\(x < \overset{ -}{x} -2s(\)其中\( \overset{ -}{x}\)是成绩的平均值，\(s\)是标准差\()\)，则认为该生测试成绩不达标，试估计该中学测试成绩不达标人数．
参考公式：\(s^{2}= \sum\limits_{i=1}^{n}(x_{i}- \overset{ -}{x} ) ^{2} p _{i} (p _{i}\)是第\(i\)组的频率\()\)，其中\( \sqrt {2}≈1.4, \sqrt {117}≈10.8\)．

查看解析收藏纠错

+选题
题型：解答题题类：模拟题难易度：易
新
年份：2020

已知数列\(\{a _{n} \}\)的前\(n\)项和为\(T _{n} = \dfrac {3}{2} n ^{2} - \dfrac {1}{2} n\)，且\(a _{n} +2+3\log _{4} b _{n} =0(n∈N*)\)．
\((1)\)求数列\(\{b _{n} \}\)的通项公式；
\((2)\)数列\(\{c _{n} \}\)满足\(c _{n} =a _{n} \boldsymbol{⋅}b _{n}\)，求数列\(\{c _{n} \}\)的前\(n\)项和\(S _{n}\)．

查看解析收藏纠错

+选题

题型：解答题题类：模拟题难易度：易

新

年份：2020

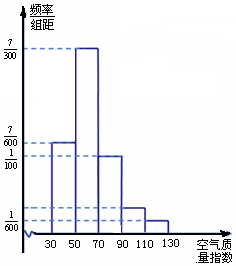某市积极贯彻落实国务院\(《\)“十三五”节能减排综合工作方案\(》\)，空气质量明显改善．该市生态环境局统计了某月\((30\)天\()\)空气质量指数，绘制成如图频率分布直方图．已知空气质量等级与空气质量指数对照如表：

空气质量指数	\((0 , 50]\)	\((50 , 100]\)	\((100 , 150]\)	\((150 , 200]\)	\((200 , 300]\)	\(300\)以上
空气质量等级	一级 \((\)优\()\)	二级 \((\)良\()\)	三级 \((\)轻度污染\()\)	四级 \((\)中度污染\()\)	五级 \((\)重度污染\()\)	六级 \((\)严重污染\()\)

\((1)\)在这\(30\)天中随机抽取一天，试估计这一天空气质量等级是优或良的概率；
\((2)\)根据体质检查情况，医生建议：当空气质量指数高于\(90\)时，某市民不宜进行户外体育运动．试问：该市民在这\(30\)天内，有多少天适宜进行户外体育运动？

查看解析收藏纠错

+选题

题型：解答题题类：模拟题难易度：易
新
年份：2020

若偶函数\(f(x)=\sin (x+θ)-2\cos x(0 < θ < π)\)，则\(θ=\)______，\(f(x)\)的最大值为______．

查看解析收藏纠错

+选题
题型：解答题题类：模拟题难易度：易
新
年份：2020

已知函数\(f(x)=2\sin (x+ \dfrac {π}{3} )\cos x\)，\(x∈R\)．
\((1)\)求函数\(f(x)\)的最小正周期；
\((2)\)当\(x∈[- \dfrac {π}{4} , \dfrac {π}{4} ]\)时，求函数\(f(x)\)的最大值与最小值．

查看解析收藏纠错

+选题

高中

选择知识点

服务介绍

帮助中心

分组	频数
\([30 , 32)\)	\(6\)
\([32 , 34)\)	\(10\)
\([34 , 36)\)	\(20\)
\([36 , 38)\)	\(30\)
\([38 , 40)\)	\(18\)
\([40 , 42)\)	\(12\)
\([42 , 44)\)	\(4\)