题型：解答题 题类：期中考试 难易度：较易
新年份：2021
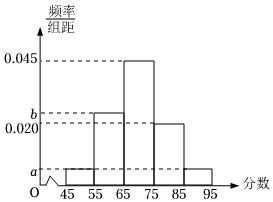第\(19\)届亚运会将于\(2022\)年\(9\)月在杭州举行，志愿者的服务工作是亚运会成功举办的重要保障．某高校承办了杭州志愿者选拔的面试工作．现随机抽取了\(100\)名候选者的面试成绩，并分成五组：第一组\([45,55),\)第二组\([55,65),\)第三组\([65,75),\)第四组\([75,85),\)第五组\([85,95),\)绘制成如图所示的频率分布直方图．已知第三、四、五组的频率之和为\(0.7\)，第一组和第五组的频率相同．题型：解答题 题类：单元测试 难易度：较易
新年份：2021
减轻雾霾的雾炮机的工作原理与建筑工地上用高压水枪除尘的原理相似，某公司为测试他们的雾炮机的除尘效果，经过\(100\)次测试得到了某雾炮机除尘率的频数分布表：
除尘率\(/％\) | \([0,5)\) | \([5,10)\) | \([10,15)\) | \([15,20)\) | \([20,25)\) | \([25,30)\) | \([30,35]\) |
频数 | \(10\) | \(15\) | \(10\) | \(25\) | \(20\) | \(15\) | \(5\) |
\((1)\)估计除尘率在\(10％\)以下的概率；
\((2)\)若除尘率达到\(18％\)以上，则认定雾炮机除尘有效，请根据以上数据估计该雾炮机除尘有效的概率．
题型：解答题 题类：单元测试 难易度：较易
新年份：2021
某学校为了解高一新生的体质健康状况，对学生的体质进行了测试．现从男、女生中各随机抽取\(20\)人，把他们的测试数据，按照《国家学生体质健康标准》整理成下表．规定：总分\(\geqslant 60\)，体质健康为合格．
等级 | 总分 | 男生人数 | 男生平均分 | 女生人数 | 女生平均分 |
优秀 | \([90,100]\) | \(5\) | \(91.3\) | \(2\) | \(91\) |
良好 | \([80,89.9]\) | \(4\) | \(83.9\) | \(4\) | \(84.1\) |
及格 | \([60,79.9]\) | \(8\) | \(70\) | \(11\) | \(70.2\) |
不及格 | \(60\)以下 | \(3\) | \(49.6\) | \(3\) | \(49.1\) |
总计 | \(-\) | \(20\) | \(-\) | \(20\) | \(-\) |
\((\)\(1)\)从样本中随机选取一名学生，求这名学生体质健康等级是合格的概率；
\((2)\)从男生样本和女生样本中各随机选取一人，求恰有一人的体质健康等级是优秀的概率；
题型：解答题 题类：单元测试 难易度：较易
新年份：2021
已知圆\(O\)：\(x^{2}+y^{2}=r^{2}(r>0)\)与直线\(x-y+2\sqrt{2}=0\)相切．
\((1)\)求圆\(O\)的方程；
\((2)\)若圆\(O\)截过点\((1,\dfrac{\sqrt{3}}{3})\)的直线\(l\)所得的弦长为\(2\sqrt{3}\)，求直线\(l\)的方程；
\((3)\)设圆\(O\)与\(x\)轴的负半轴的交点为\(A\)，过点\(A\)作两条斜率分别为\(k_{1}\)，\(k_{2}\)的直线交圆\(O\)于\(B\)，\(C\)两点，且\(k_{1}k_{2}=-2\)，试证明直线\(BC\)恒过一个定点，并求出该定点的坐标．
