代数-数学-知识点同步搜题

选择知识点

题型：

全部选择题填空题解答题

难易程度：

全部易较易中档较难难

题类筛选：

全部历年真题模拟题期末考试期中考试月考试卷单元测试其他

年份：

全部 2025 2024 2023 2022 2021 2020 更早

总题量：4791选择本页全部试题

题型：解答题题类：期中考试难易度：较易
新
年份：2021

已知圆\(C\)经过点\(A(3,-2)\)和\(B(1,0)\)，且圆心在直线\(x+y+1=0\)上．
\((1)\)求圆\(C\)的方程；
\((2)\)若直线\(l\)：\(kx-y-k+3=0\)与圆\(C\)交于不同的两点\(A\)，\(B\)，求实数\(k\)的取值范围．

查看解析收藏纠错

+选题
题型：解答题题类：期中考试难易度：较易
新
年份：2021

已知直线\(l\)经过直线\(2x-y+1=0\)与直线\(x+2y-7=0\)的交点\(P.\)
\((1)\)若两定点\(A(6,-6)\)、\(B(2,4)\)到直线\(l\)的距离相等，求直线\(l\)的方程；
\((2)\)若直线\(l\)与圆\(Q\)：\((x+1)²+(y-2)²=9\)相交于\(C\)，\(D\)两点，求弦长的最小值及此时直线\(l\)的方程．

查看解析收藏纠错

+选题
题型：解答题题类：期中考试难易度：较易
新
年份：2021

设椭圆\(M\)：\(\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1(a>b>0)\)的左顶点为\(A\)、中心为\(O.\)若椭圆\(M\)过点\(P(-\dfrac{1}{2},\dfrac{1}{2})\)，且\(AP⊥PO.\)
\((1)\)求椭圆\(M\)的方程；
\((2)\)过点\(A\)作两条斜率分别为\(k_{1}\)，\(k_{2}\)的直线交椭圆\(M\)于\(D\)，\(E\)两点，且\(k_{1}k_{2}=1\)，求证：直线\(DE\)恒过一个定点．

查看解析收藏纠错

+选题
题型：解答题题类：期中考试难易度：较易
新
年份：2021

已知直线\(l\)：\(x-ty-1=0\)，圆\(C\)：\((x-k)^{2}+(y-2k+1)^{2}=4.\)
\((1)\)若\(t=1\)，直线\(l\)与圆\(C\)交于\(A\)、\(B\)两点，且\(AB=\sqrt{2}CA\)，求圆\(C\)的标准方程；
\((2)\)是否存在实数\(t\)，使得直线\(l\)被圆\(C\)所截得的弦长为定值？若存在，求出\(t\)的值；若不存在，请说明理由．

查看解析收藏纠错

+选题
题型：解答题题类：期中考试难易度：较易
新
年份：2021

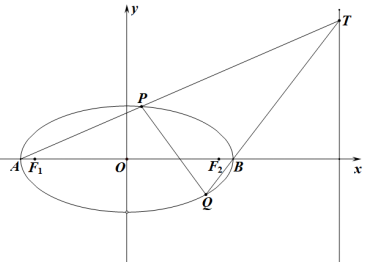已知椭圆\(E\)：\(\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1(a>b>0)\)的左、右焦点为分别为\(F_{1}\)、\(F_{2}\)，离心率为\(\dfrac{\sqrt{3}}{2}\)，点\(M\)为椭圆上一点，且\(\triangle F_{1}MF_{2}\)面积的最大值为\(\sqrt{3}.\)
\((1)\)求椭圆\(E\)的标准方程；
\((2)\)若\(A\)、\(B\)分别为椭圆的左、右端点，点\(T(4,m)(m≠0)\)，直线\(TA\)、\(TB\)分别交椭圆\(E\)于\(P\)、\(Q\)两点．证明：直线\(PQ\)过定点．

查看解析收藏纠错

+选题
题型：解答题题类：期中考试难易度：较易
新
年份：2021

已知二次函数\(f(x)=ax^{2}+bx+c\)，满足\(f(0)=f(1)=0\)，且\(f(x)\)的最小值是\(-\dfrac{1}{4}.\)
\((1)\)求函数\(f(x)\)的解析式；
\((2)\)设函数\(g(x)=x^{2}+5x-2\)，函数\(h(x)=f(x)-g(x)\)，求函数\(h(x)\)在区间\([-2,5]\)上的最值．

查看解析收藏纠错

+选题
题型：解答题题类：期中考试难易度：较易
新
年份：2021

集合\(A=\{x|x^{2}-5x-14\leqslant 0\}\)，\(B=\{x|m+1< x< 2m-1\}.\)
\((1)\)当\(m=5\)时，求\(A∪B\)；
\((2)\)当\(B≠\varnothing\)时，若\(A∩B=B\)，求实数\(m\)的取值范围．

查看解析收藏纠错

+选题
题型：解答题题类：期中考试难易度：较易
新
年份：2021

已知奇函数\(f(x)=\dfrac{ax+b}{x^{2}+1}\)是定义在区间\([-1,1]\)上的增函数，且\(f(\dfrac{1}{2})=\dfrac{2}{5}.\)
\((1)\)求函数\(f(x)\)的解析式；
\((2)\)求不等式\(f(x-1)< f(-x)\)的解集．

查看解析收藏纠错

+选题
题型：解答题题类：期中考试难易度：较易
新
年份：2021

已知函数\(f(x)=-x^{2}+ax-2\)，\(x\in[1,3].\)
\((1)\)当\(a=4\)时，求函数\(f(x)\)的值域；
\((2)\)若\(f(x)< 0\)恒成立，求实数\(a\)的取值范围．

查看解析收藏纠错

+选题
题型：解答题题类：期中考试难易度：较易
新
年份：2021

集合\(A=\{x|-6x^{2}-x+2>0\}\)，\(B=\{x|x^{2}-5x+6\geqslant 0\}.\)
\((1)\)求\(A∪B\)；
\((2)\)求\((∁_{R}A)∩B.\)

查看解析收藏纠错

+选题

高中

选择知识点

服务介绍

帮助中心