选择知识点

设正项数列\(\left\{{{a}_{n}}\right\}\)的前\(n\)项和为\({{S}_{n}}\)，且\({{a}_{1}}=1\)，当\(n\geqslant 2\)时，\({{a}_{n}}=\sqrt{{{S}_{n}}}+\sqrt{{{S}_{n-1}}}.\)

\((1)\)求数列\(\left\{{{a}_{n}}\right\}\)的通项公式；

\((2)\)设数列\(\left\{{{b}_{n}}\right\}\)满足\(\dfrac{{{b}_{1}}}{{{2}^{1}}}+\dfrac{{{b}_{2}}}{{{2}^{2}}}+\cdots+\dfrac{{{b}_{n-1}}}{{{2}^{n-1}}}+\dfrac{{{b}_{n}}}{{{2}^{n}}}={{a}_{n}}\)，求\(\left\{{{b}_{n}}\right\}\)的前\(n\)项和\({{T}_{n}}.\)

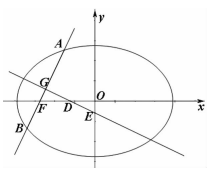
如图，椭圆\(\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1\left(a>b>0\right)\)的左焦点为\(F\)，过点\(F\)的直线交椭圆于\(A\)，\(B\)两点，\(\left|AF\right|\)的最大值为\(M\)，\(\left|BF\right|\)的最小值为\(m\)，满足\(M\bullet m=\dfrac{3}{4}{{a}^{2}}.\)

\((1)\)若线段\(AB\)垂直于轴时，\(\left|AB\right|=\dfrac{3}{2}\)，求椭圆的方程；

\((2)\)设线段\(AB\)的中点为\(G\)，\(AB\)的垂直平分线与\(x\)轴和\(y\)轴分别交于\(D\)，\(E\)两点，\(O\)是坐标原点，记\(\Delta GFD\)的面积为\({{S}_{1}}\)，\(\Delta OED\)的面积为\({{S}_{2}}\)，求\(\dfrac{{{S}_{1}}}{{{S}_{2}}}\)的取值范围.

已知全集\(U=\text{R}\)，集合\(A=\{x\in\text{R}|\dfrac{1}{3}< {{(\dfrac{1}{3})}^{x}}< \text{9}\}\)，集合\(B=\{x\in\text{R}|{{x}^{2}}-\text{2}x-a\leqslant 0\}\)，集合\(C=\{x\in\text{R}|m-1< x< 2m\}\)，\(A∩B=\{x\in R|-1⩽x< 1\}.\)

\((1)\)求集合\(B\)；

\((2)\)求\(({∁}_{\;{\rm R}}B)∪A\)；

\((3)\)若\(B∪C=B\)，求实数\(m\)的取值范围．

已知偶函数\(f(x)\)的定义域为\((-{\rm∞},0)∪(0,+{\rm∞})\)，\(f(-\text{2})=\dfrac{\text{3}}{\text{2}}\)，当\(x\in(0,+\infty)\)时，函数\(f(x)=x-\dfrac{m}{x}.\)

\((1)\)求实数\(m\)的值；

\((2)\)当\(x\in(-\infty,\text{0})\)时，求函数\(f(x)\)的解析式；

\((3)\)判断并证明函数\(f(x)\)在区间\((0,+\infty)\)的单调性．

已知函数\(f(x)={{x}^{2}}-(m+2)x+2m\)，\(m\in\text{R}.\)

\((1)\)若\(f(x)\geqslant 0\)对任意的\(x\in\text{R}\)恒成立，求实数\(m\)的取值范围；

\((2)\)若\(f(x)\)在\((-\infty,3)\)上单调递减，求实数\(m\)的取值范围；

\((3)\)解不等式\(f(x)>0.\)

某科研单位在研发某种合金产品的过程中发现了一种新型合金材料，由大数据分析得到该产品的性能指标值\(y(y\)值越大产品性能越好\()\)与这种新型合金材料的含量\(x(\)单位：克\()\)的关系：当\(0\leqslant x< 8\)时，\(y\)是\(x\)的二次函数；当\(x\geqslant 8\)时，\(y={{(\dfrac{1}{2})}^{x-t}}.\)测得的部分数据如下表所示：

\((1)\)求\(y\)关于\(x\)的函数解析式；

\((2)\)求该新型合金材料的含量\(x\)为何值时产品性能达到最佳．

若对于任意\({{x}_{1}},{{x}_{2}}\in\text{R}\)，使得\({{x}_{1}}-{{x}_{2}}\in W\)，都有\(f({{x}_{1}})-f({{x}_{2}})\in W\)，则称\(f(x)\)是\(W\)陪伴的．

\((1)\)判断\(f(x)=3x-1\)是否为\([0,+\infty)\)陪伴的，并证明；

\((2)\)若\(f(x)={{a}^{x}}(a>0,a\neq 1)\)是\([0,+\infty)\)陪伴的，求\(a\)的取值范围；

\((3)\)若\(f(x)\)是\(\{2\}\)陪伴的，且是\((0,+\infty)\)陪伴的，求证：\(f(x)\)是\((2,4)\)陪伴的．