代数-数学-知识点同步搜题

选择知识点

题型：

全部选择题填空题解答题

难易程度：

全部易较易中档较难难

题类筛选：

全部历年真题模拟题期末考试期中考试月考试卷单元测试其他

年份：

全部 2022 2021 2020 2019 2018 2017 更早

总题量：67选择本页全部试题

题型：解答题题类：历年真题难易度：易

年份：2018

已知函数\(f(x)=\sin (ωx+φ)(ω > 0,|φ|\leqslant \dfrac {π}{2})\)的最小正周期为\(π\)，且\(x= \dfrac {π}{12}\)为\(f(x)\)图象的一条对称轴．
\((1)\)求\(ω\)和\(φ\)的值；
\((2)\)设函数\(g(x)=f(x)+f(x- \dfrac {π}{6})\)，求\(g(x)\)的单调递减区间．

查看解析收藏纠错

+选题
题型：解答题题类：历年真题难易度：易

年份：2018

为迎接即将举行的集体跳绳比赛，高一年级对甲、乙两个代表队各进行了\(6\)轮测试，测试成绩\((\)单元：次\(/\)分钟\()\)如下表：

\((1)\)补全茎叶图，并指出乙队测试成绩的中位数和众数\(;\)

\((2)\)试用统计学中的平均数和方差知识对甲、乙两个代表队的测试成绩进行分析．

查看解析收藏纠错

+选题
题型：解答题题类：历年真题难易度：易

年份：2018

在\(\triangle ABC\)中，角\(A\)，\(B\)，\(C\)的对边分别为\(a\)，\(b\)，\(c\)，且\((2a-b)⋅\cos C=c⋅\cos B\)．
\((1)\)求角\(C\)的大小；
\((2)\)若\(c=2\)，\(\triangle ABC\)的面积为\( \sqrt {3}\)，求该三角形的周长．

查看解析收藏纠错

+选题
题型：解答题题类：历年真题难易度：易

年份：2018

(2018•山东) (本小题6分) 已知函数\( f\left(x\right)={x}^{2}+(m-1)x+4\), 其中m为常数。
(1)若函数f(x)在区间( -∞，0 )上单调递减，求实数m的取值范围；
(2)若∀x∈R，都有f(x)>0，求实数m的取值范围。
.

查看解析收藏纠错

+选题
题型：解答题题类：历年真题难易度：易

年份：2018

(2018•山东) (本小题8分) 已知在等比数列\( {a}_{n}\)中，\( {a}_{2}=\frac{1}{4}\)，\( {a}_{5}=\frac{1}{32}\)
(1)求数列\( {a}_{n}\)的通项公式：
(2)若数列\( {b}_{n}\)满足\( {b}_{n}={a}_{n}+n\)，求\( {b}_{n}\)的前 n 项和\( {S}_{n}\)。

查看解析收藏纠错

+选题
题型：解答题题类：历年真题难易度：易

年份：2018

如图，在四棱锥\(P-ABCD\)中，\(O\)为\(AC\)与\(BD\)的交点，\(AB⊥\)平面\(PAD\)，\(\triangle PAD\)是正三角形， \(DC/\!/AB\)，\(DA=DC=2AB\)．

\((1)\)若点\(E\)为棱\(PA\)上一点，且\(OE/\!/\)平面\(PBC\)，求\( \dfrac{AE}{PE}\)的值；

\((2)\)求证：平面\(PBC⊥\)平面\(PDC\)．

查看解析收藏纠错

+选题
题型：解答题题类：历年真题难易度：易

年份：2018

在\(\triangle ABC\)中，角\(A\)，\(B\)，\(C\)所对的边分别为\(a\)，\(b\)，\(c\)，且\( \dfrac {\tan B}{\tan A}+1= \dfrac {2c}{a}\)．
\((1)\)求\(B\)；
\((2)\)若\(\cos (C+ \dfrac {π}{6})= \dfrac {1}{3}\)，求\(\sin A\)的值．

查看解析收藏纠错

+选题
题型：解答题题类：历年真题难易度：易

年份：2018

某市随机抽取部分企业调查年度缴税情况\((\)单位：万元\()\)，将所得数据绘制成频率分布直方图\((\)如图\()\)，年度缴税的范围是\([0,100]\)，样本数据分组为第一组：\([0,20)\)，第二组：\([20,40)\)，第三组：\([40,60)\)，第四组：\([60,80)\)，第五组：\([80,100]\)．

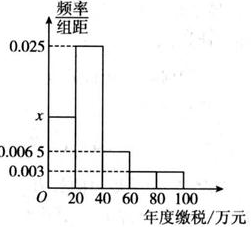
\((1)\)求频率分布直方图中\(x\)的值；
\((2)\)如果年度缴税不少于\(60\)万元的企业可以申请政策优惠，若共抽取\(1200\)家企业，试估计有多少家企业可以申请政策优惠；

\((3)\)若从第一组和第二组中利用分层抽样的方法抽取\(6\)家企业，试求在这\(6\)家企业中任选\(2\)家，这\(2\)家企业年度缴税在同一组的概率．

查看解析收藏纠错

+选题
题型：解答题题类：历年真题难易度：易

年份：2018

\(\Delta ABC\)的内角\(A\)，\(B\)，\(C\)的对边分别为\(a\)，\(b\)，\(c\)，已知\(2\cos C(a\cos B+b\cos A)=c.\)

\((I)\)求\(C\)；

\((II)\)若\(c=\sqrt{7},\Delta ABC\)的面积为\(\dfrac{3\sqrt{3}}{2}\)，求\(\vartriangle ABC\)的周长．

查看解析收藏纠错

+选题
题型：解答题题类：历年真题难易度：易

年份：2018

某高校共有\(15000\)名学生，其中男生\(10500\)名，女生\(4500\)名\(.\)为调查该校学生每周平均运动时间的情况，采用分层抽样的方法，收集了\(300\)名学生每周平均运动时间\((\)单位：小时\()\)的样本数据．

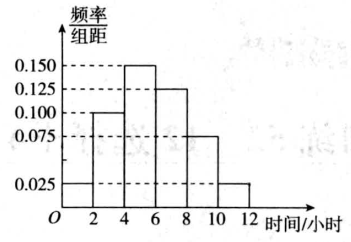
\((1)\)应收集多少名女生的样本数据\(?\)

\((2)\)根据这\(300\)个样本数据，得到学生每周平均运动时间的频率分布直方图\((\)如图所示\()\)，其中样本数据的分组区间为：\([0,2]\)，\((2,4]\)，\((4,6]\)，\((6,8]\)，\((8,10]\)，\((10,12].\)估计该校学生每周平均运动时间超过\(4\)小时的概率．

\((3)\)在样本数据中，有\(60\)名女生的每周平均运动时间超过\(4\)小时，请作出每周平均运动时间与性别的\(2×2\)列联表，并判断是否有\(95％\)的把握认为“该校学生的每周平均运动时间与性别有关”．

查看解析收藏纠错

+选题

高中

选择知识点

服务介绍

帮助中心