题型：解答题 题类：历年真题 难易度：较难
新年份：2019
某集团公司为了加强企业管理，树立企业形象，考虑在公司内部对迟到现象进行处罚.现在员工中随机抽取200人进行调查，当不处罚时，有80人会迟到，处罚时，得到如下数据：
处罚金额 | 50 | 100 | 150 | 200 |
迟到的人数 | 50 | 40 | 20 | 0 |
若用表中数据所得频率代替概率.
（Ⅰ）当处罚金定为100元时，员工迟到的概率会比不进行处罚时降低多少？
（Ⅱ）将选取的200人中会迟到的员工分为
，
两类：类员工在罚金不超过100元时就会改正行为；类是其他员工.现对类与类员工按分层抽样的方法抽取4人依次进行深度问卷，则前两位均为类员工的概率是多少？
题型：解答题 题类：历年真题 难易度：较难
新年份：2019
题型：解答题 题类：历年真题 难易度：较难
新年份：2019
| 983 | 972 | 966 | 992 | 1010 | 1008 | 954 | 952 | 969 |
| 968 | 998 | 1001 | 1006 | 957 | 950 | 969 | 971 | 975 |
| 952 | 959 | 987 | 1011 | 1000 | 997 | 961 |
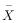=978.72g，标准差是20.16g，认定面包师在制作过程中偷工减料，并果断举报给质检部门，质检员对面包师做了处罚，面包师也承认自己的错误，并同意做出改正．
．
，求f（x）的取值范围；
，求△ABC面积的最大值． 
的图象关于原点对称．
）cosx，将函数y＝g（x）的图象向左平移
个单位得到y＝f（x）的图象．
=10．
的最小正整数n的值． 
．
是首项为1的递减数列，且
．
求数列
若
，求数列
的前n项和
． 
，a1=1． 
，若{bn}是递增数列，求实数a的取值范围． 