题型：解答题 题类：模拟题 难易度：难
年份：2018
已知函数\(f\left( x \right)=a{{x}^{2}}-bx+1\)，\(f\left( 1 \right)=0\)，且\(f\left( x \right)\geqslant 0\)在\(R\)上恒成立，\(g\left( x \right)=1-{\ln }x\)．
\((\)Ⅰ\()\) 求\(y=f\left( x \right)\)的解析式；
\((\)Ⅱ\()\) 若有\(f\left( m \right)=g\left( n \right)\)，求实数\(n\)的取值范围；
\((\)Ⅲ\()\)求证：\(y=f\left( x \right)\)与\(y=g\left( x \right)\)图像在区间\(\left[ 1,{e} \right]\)有唯一公共点．
题型：解答题 题类：模拟题 难易度：难
年份：2018
已知集合\(M\)是同时满足下列两个性质的函数的全体：
\(①\)函数\(f(x)\)的单调函数；
\(②\)在函数\(f(x)\)在定义域内存在闭区间\(\left[ a,b \right]\)使得\(f(x)\)在\(\left[ a,b \right]\)的最小值为\(\dfrac{a}{2}\)，最大值为\(\dfrac{b}{2}\)；
请解答以下问题：
\((1)\)判断\(g(x)=-{{x}^{3}}\)是否属于\(M\)？并说明理由；请找出满足\(②\)的闭区间\(\left[ a,b \right]\)；
\((2)\)已知函数\(h(x)=\sqrt{x-1}+t\)，若\(h(x)\in M\)，求\(t\)的范围。
题型：解答题 题类：模拟题 难易度：难
年份：2018
如图，已知椭圆\(O:\dfrac{{{x}^{2}}}{4}+{{y}^{2}}=1\)的右焦点为\(F\)，\(B\)，\(C\)分别为椭圆\(O\)的上、下顶点，\(P\)是直线\(l:y=-2\)上的一个动点\((\)与\(y\)轴交点除外\()\)，直线\(PC\)交椭圆\(O\)于另一点\(M\)．
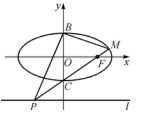
\((1)\) 当直线\(PM\)过椭圆的右焦点\(F\)时，求\(\triangle FBM\)的面积．
\((2)①\)记直线\(BM\)，\(BP\)的斜率分别为\(k_{1}\)，\(k_{2}\)，求证：\(k_{1}·k_{2}\)为定值\(;\)\(②\)求\(\overrightarrow{{PB}}\)\(·\)\(\overrightarrow{{PM}}\)的取值范围．
题型：解答题 题类：模拟题 难易度：难
年份：2018
题型：解答题 题类：模拟题 难易度：难
年份：2018
在直角坐标系\(xOy\)中，以坐标原点\(O\)为极点，以\(x\)轴正半轴为极轴，建立极坐标系，直线\({{l}_{1}}\)的极坐标方程为\(\rho =\dfrac{-1}{{\sin }\theta +a{\cos }\theta }\)，\({{l}_{2}}\)的极坐标方程为\(\rho =\dfrac{1}{{\cos }\theta -a{\sin }\theta }\)．
\((1)\)求直线\({{l}_{1}}\)与\({{l}_{2}}\)的交点的轨迹\(C\)的方程；
\((2)\)若曲线\(C\)上存在\(4\)个点到直线\({{l}_{1}}\)的距离相等，求实数\(a\)的取值范围．
．
如图，在四棱锥P-ABCD中，底面ABCD为平行四边形，已知PA=AC=2，∠PAD=∠DAC=60°，CE⊥AD于E．
如图所示，\(\triangle ABC\)和\(\triangle BCE\)是边长为\(2\)的正三角形，且平面\(ABC⊥\)平面\(BCE\)，\(AD⊥\)平面\(ABC\)，\(AD=2 \sqrt {3}\)． 
