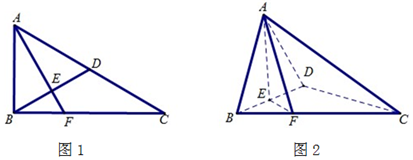
题型：解答题 题类：月考试卷 难易度：易
新年份：2020
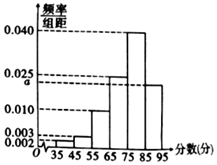某学校高三年级在开学时举行了入学检测．为了了解本年级学生寒假期间历史的学习情况，现从年级\(1000\)名文科生中随机抽取了\(200\)名学生本次考试的历史成绩，得到他们历史分数的频率分布直方图如图．已知本次考试高三年级历史成绩分布区间为\([35 , 95]\)．题型：解答题 题类：月考试卷 难易度：易
新年份：2020
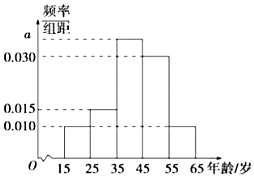“绿水青山就是金山银山”的理念越来越深入人心，据此，某网站调查了人们对生态文明建设的关注情况，调查数据表明，参与调查的人员中关注生态文明建设的约占\(80\%.\)现从参与调查的关注生态文明建设的人员中随机选出\(200\)人，并将这\(200\)人按年龄\((\)单位：岁\()\)分组：第\(1\)组\([15 , 25)\)，第\(2\)组\([25 , 35)\)，第\(3\)组\([35 , 45)\)，第\(4\)组\([45 , 55)\)，第\(5\)组\([55 , 65]\)，得到的频率分布直方图如图所示．题型：解答题 题类：月考试卷 难易度：易
新年份：2020
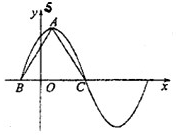函数\(f(x)=6\cos ^{2} \dfrac {ωx}{2} + \sqrt {3} \sin ωx(ω > 0)\)在一个周期内的图象如图所示，\(A\)为图象的最高点，\(B\)，\(C\)为图象与\(x\)轴的交点，且\(\triangle ABC\)为正三角形题型：解答题 题类：月考试卷 难易度：易
新年份：2020
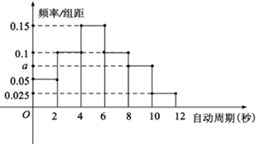我国在贵州省平塘县境内修建的\(500\)米口径球面射电望远镜\((FAST)\)是目前世界上最大单口径射电望远镜．使用三年来，已发现\(132\)颗优质的脉冲星候选体，其中有\(93\)颗已被确认为新发现的脉冲星．脉冲星是上世纪\(60\)年代天文学的四大发现之一，脉冲星就是正在快速自转的中子星，每一颗脉冲星每两脉冲间隔时间\((\)脉冲星的自转周期\()\)是一定的，最小小到\(0.0014\)秒，最长的也不过\(11.765735\)秒．某一天文研究机构观测并统计了\(93\)颗已被确认为新发现的脉冲星的自转周期，绘制了如图的频率分布直方图．题型：解答题 题类：月考试卷 难易度：易
新年份：2020
某校为于了解\(2020\)年新冠肺炎疫情“停课不停学”期间高三学生平均每天学习的时间\((\)单位：小时\()\)，从本校随机抽取了\(100\)名学生进行调查，根据收集的数据，得到学生每天学习时间的频率分布直方图，如图所示，若每天学习时间不超过\(10\)小时的有\(45\)人．
已知\(\triangle ABC\)中，\(AB= \sqrt {3}\)，\(D\)是边\(BC\)上一点，\(AD= \sqrt {2}\)，\(∠ADC= \dfrac {π}{3}\)，\(∠DAC= \dfrac {5π}{12}\)．