题型:解答题 题类:模拟题 难易度:中档
新年份:2019
 中国独有的文书工具,即笔、墨、纸、砚,有文房四宝之名,起源于南北朝时期.其中宣纸是文房四宝的一种,宣纸“始于唐代,产于泾县”,因唐代泾县隶属宣州管辖,故因地得名宣纸.宣纸按质量等级分为:正牌(优等品)、副牌(合格品)、废品三等.某公司生产的宣纸为纯手工制作,年产宣纸10000刀(1刀=100张),该公司按照某种质量指标x给宣纸确定等级如表所示:
中国独有的文书工具,即笔、墨、纸、砚,有文房四宝之名,起源于南北朝时期.其中宣纸是文房四宝的一种,宣纸“始于唐代,产于泾县”,因唐代泾县隶属宣州管辖,故因地得名宣纸.宣纸按质量等级分为:正牌(优等品)、副牌(合格品)、废品三等.某公司生产的宣纸为纯手工制作,年产宣纸10000刀(1刀=100张),该公司按照某种质量指标x给宣纸确定等级如表所示:| x的范围 | (44,48]∪(52,56] | (48,52] | [0,44]∪(56,60] |
| 质量等级 | 副牌 | 正牌 | 废品 |
| x的范围 | (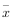 -2, -2,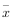 +2) +2) | (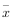 -6, -6,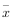 +6) +6) |
| 频率 | 0.6827 | 0.9545 |
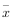 为质量指标x的平均值,但是由于人们对传统手工工艺的认可,改进后的正牌和副牌宣纸的利润都将下降3元/张,请该公司是否购买这种机器,请你为公司提出合理建议,并说明理由.(同一组的数据用该组区间的中点值作代表)
为质量指标x的平均值,但是由于人们对传统手工工艺的认可,改进后的正牌和副牌宣纸的利润都将下降3元/张,请该公司是否购买这种机器,请你为公司提出合理建议,并说明理由.(同一组的数据用该组区间的中点值作代表) 题型:解答题 题类:模拟题 难易度:难
新年份:2019
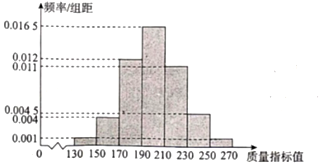 某高科技公司投人1000万元研发某种产品,大规模投产后,每天在产品进入库房前,都需做严格的质量检验.为此,检验人员从当天生产的产品中随机抽取80件,检测一项关键的质量指标值(记为X),由检测结果得到如下样本频率分布直方图.
某高科技公司投人1000万元研发某种产品,大规模投产后,每天在产品进入库房前,都需做严格的质量检验.为此,检验人员从当天生产的产品中随机抽取80件,检测一项关键的质量指标值(记为X),由检测结果得到如下样本频率分布直方图.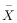 、方差s2(同一组数据用该区间的中点值作代表)可作为μ,σ2的估计值.利用该正态分布,求P(X>175.5)(精确到0.01);
、方差s2(同一组数据用该区间的中点值作代表)可作为μ,σ2的估计值.利用该正态分布,求P(X>175.5)(精确到0.01);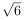 ≈2.45,P(μ-σ<X≤μ+σ)=0.683,P(μ-2σ<X≤μ+2σ)=0.954
≈2.45,P(μ-σ<X≤μ+σ)=0.683,P(μ-2σ<X≤μ+2σ)=0.954