代数-数学-知识点同步搜题

选择知识点

题型：

全部选择题填空题解答题

难易程度：

全部易较易中档较难难

题类筛选：

全部历年真题模拟题期末考试期中考试月考试卷单元测试其他

年份：

全部 2025 2024 2023 2022 2021 2020 更早

总题量：880选择本页全部试题

题型：选择题题类：月考试卷难易度：中档
新测
年份：2020

已知直线\(l\)与圆\(C\)：\(x ^{2} +y ^{2} -2x-4y=0\)相交于\(A\)，\(B\)两点，\(O\)为坐标原点，若锐角\(\triangle ABC\)的面积为\( \dfrac {12}{5}\)，则\(\sin ∠AOB= (\:\:\:\:)\)

A.\( \dfrac {12}{25}\) B.\( \dfrac {3}{5}\) C.\( \dfrac {3}{4}\) D.\( \dfrac {4}{5}\)

查看解析收藏纠错

+选题
题型：选择题题类：月考试卷难易度：中档
新测
年份：2020

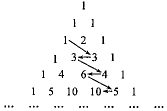如图，在杨辉三角中，斜线\(l\)的上方从\(1\)按箭头所示方向可以构成一个“锯齿形”数列：\(1\)，\(3\)，\(3\)，\(4\)，\(6\)，\(5\)，\(10\)，\(…\)，将该数列中的奇数项依次取出组成一个新的数列\(\{a _{n} \}\)，则\( \dfrac {1}{a_{1}} + \dfrac {1}{a_{2}} + \dfrac {1}{a_{3}} +……+ \dfrac {1}{\;_{a_{2020}}} = (\:\:\:\:)\)

A.\( \dfrac {2020}{2021}\) B.\( \dfrac {2019}{2020}\) C.\( \dfrac {4021}{2020}\) D.\( \dfrac {4040}{2021}\)

查看解析收藏纠错

+选题
题型：解答题题类：月考试卷难易度：中档
新
年份：2020

已知\(F _{1}\)，\(F _{2}\)分别为椭圆\(C\)：\( \dfrac {x^{2}}{a^{2}} + \dfrac {y^{2}}{b^{2}} =1(a > b > 0)\)的左右焦点，点\(P ( \dfrac { \sqrt {6}}{2}, \dfrac {1}{2})\)在椭圆\(C\)上，且\(|PF _{l} |+|PF _{2} |=2 \sqrt {2}\)．
\((1)\)求椭圆\(C\)的方程；
\((2)\)设\(A\)为椭圆\(C\)的左顶点，过点\(F _{2}\)的直线\(l\)椭圆\(C\)于\(M\)，\(N\)两点，记直线\(AM\)，\(AN\)的斜率分别为\(k _{1}\)，\(k _{2}\)，若\(k _{1} +k _{2} =3\)，求直线\(l\)方程．

查看解析收藏纠错

+选题
题型：选择题题类：月考试卷难易度：中档
新测
年份：2020

在直角三角形\(ABC\)中，\(∠C= \dfrac {π}{2}\)，\(BC=1\)，点\(M\)在边\(AC\)上，且\(AM=2MC\)，则\(\tan ∠MBA\)的最大值为\((\:\:\:\:)\)

A.\( \dfrac {1}{3}\) B.\( \dfrac { \sqrt {3}}{3}\) C.\(1\) D.\( \sqrt {3}\)

查看解析收藏纠错

+选题
题型：解答题题类：月考试卷难易度：中档
新
年份：2020

已知椭圆\(C\)的中心在原点，焦点在坐标轴上，直线\(y= \dfrac {3}{2} x\)与椭圆\(C\)在第一象限内的交点是\(M\)，点\(M\)在\(x\)轴上的射影恰好是椭圆\(C\)的右焦点\(F _{2}\)，椭圆\(C\)的另一个焦点是\(F _{1}\)，且\( \overrightarrow {MF_{1}} \boldsymbol{⋅} \overrightarrow {MF_{2}} = \dfrac {9}{4}\)．
\((1)\)求椭圆\(C\)的方程；
\((2)\)已知圆\(F _{1}\)：\((x+1) ^{2} +y ^{2} =1\)，动圆\(P\)的圆心\(P\)在椭圆\(C\)上并且与圆\(F _{1}\)外切，直线\(l\)是圆\(P\)和圆\(F _{1}\)的外公切线，直线\(l\)与椭圆\(C\)交于\(A\)，\(B\)两点，当圆\(P\)的半径最长时，求三角形\(F _{1} AB\)的面积．

查看解析收藏纠错

+选题
题型：选择题题类：月考试卷难易度：中档
新测
年份：2020

已知双曲线\(C\)：\( \dfrac {x^{2}}{a^{2}}- \dfrac {y^{2}}{b^{2}}=1(a > 0,b > 0)\)的渐近线经过圆\(E\)：\(x ^{2} +y ^{2} -2x+4y=0\)的圆心，则双曲线\(C\)的离心率为\((\:\:\:\:)\)

A.\( \sqrt {5}\) B.\( \dfrac { \sqrt {5}}{2}\) C.\(2\) D.\( \sqrt {2}\)

查看解析收藏纠错

+选题
题型：填空题题类：月考试卷难易度：中档
新
年份：2020

已知\(x\)，\(y\)满足\( \begin{cases} 3x+y\leqslant t \\ x\geqslant \dfrac {π}{6} \\ y\geqslant 0\end{cases}\)其中\(t > \dfrac {π}{2}\)，若\(\sin (x+y)\)的最大值与最小值分别为\(1\)，\( \dfrac {1}{2}\)，则实数\(t\)的取值范围为______．

查看解析收藏纠错

+选题
题型：选择题题类：月考试卷难易度：中档
新测
年份：2020

已知圆\(x ^{2} +y ^{2} =2\)与双曲线\(C： \dfrac {x^{2}}{a^{2}}- \dfrac {y^{2}}{b^{2}}=1(a,b > 0)\)的四个交点构成四边形的面积是\(4\)，若点\(P\)是圆与双曲线在第一象限的交点，\(F\)为双曲线的右焦点，且\( \overrightarrow {OP}\cdot \overrightarrow {OF}= \dfrac { \sqrt {21}}{6}\)，\((O\)为坐标原点\()\)，则双曲线的离心率为\((\:\:\:\:)\)

A.\( \dfrac { \sqrt {21}}{3}\) B.\( \dfrac {3}{2}\) C.\( \sqrt {3}\) D.\( \sqrt {2}\)

查看解析收藏纠错

+选题
题型：解答题题类：月考试卷难易度：中档
新
年份：2020

如图，在四棱锥\(E-ABCD\)中，底面\(ABCD\)为直角梯形，其中\(CD/\!/AB\)，\(BC⊥AB\)，侧面\(ABE⊥\)平面\(ABCD\)，且\(AB=AE=BE=2BC=2CD=2\)，动点\(F\)在棱\(AE\)上，且\(EF=λFA\)．
\((1)\)试探究\(λ\)的值，使\(CE/\!/\)平面\(BDF\)，并给予证明；
\((2)\)当\(λ=1\)时，求直线\(CE\)与平面\(BDF\)所成的角的正弦值．

查看解析收藏纠错

+选题
题型：解答题题类：月考试卷难易度：中档
新
年份：2020

在直角坐标系\(xOy\)中，以坐标原点为极点，\(x\)轴非负半轴为极轴建立极坐标系，曲线\(C _{1}\)的极坐标方程为\(ρ=4\cos θ\)，曲线\(C _{2}\)的参数方程为\(\left\{\begin{array}{l}x=1+ \dfrac{ \sqrt{2}}{2}t \\ y= \dfrac{ \sqrt{2}}{2}t\end{array}\right. (t\)为参数\()\)．
\((1)\)求曲线\(C _{1}\)的直角坐标方程及曲线\(C _{2}\)的普通方程；
\((2)\)设点\(P\)的直角坐标为\((1 , 0)\)，曲线\(C _{1}\)与曲线\(C _{2}\)交于\(A\)、\(B\)两点，求\(|PA|+|PB|\)的值．

查看解析收藏纠错

+选题

高中

选择知识点

服务介绍

帮助中心