题型:解答题 题类:其他 难易度:难
年份:2018
设\({{F}_{1}},{{F}_{2}}\)分别是椭圆\(E:{{x}^{2}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1\left( 0 < b < 1 \right)\)的左、右焦点,过\({{F}_{1}}\)的直线\(l\)与\(E\)相交于\(A,B\)两点,且\(\left| A{{F}_{2}} \right|,\left| AB \right|,\left| B{{F}_{2}} \right|\)成等差数列.
\((1)\)求\(\left| AB \right|\);
\((2)\)若直线\(l\)的斜率为\(1\),求\(b\)的值.
题型:解答题 题类:其他 难易度:难
年份:2018
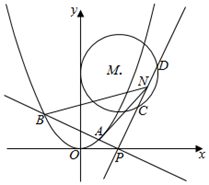
如图,抛物线\(E\):\({x}^{2}=2py(p > 0) \)的焦点为\((0, \dfrac{1}{4}) \),圆心\(M\)在射线\(y=2x(x\geqslant 0) \)上且半径为\(1\)的圆\(M\)与\(y\)轴相切.
题型:解答题 题类:其他 难易度:难
年份:2018
在平面直角坐标系\(xoy\)中,已知椭圆\(C\):\(\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1(a > b > 0)\)的离心率\(e=\dfrac{1}{2}\),左顶点为\(A\left( -4,0 \right)\),过点\(A\)作斜率为\(k\left( k\ne 0 \right)\)的直线\(l\)交椭圆\(C\)于点\(D\),交\(y\)轴于点\(E\).
\((1)\)求椭圆\(C\)的方程;
\((2)\)已知\(P\)为\(AD\)的中点,是否存在定点\(Q\),对于任意的\(k\left( k\ne 0 \right)\)都有\(OP\bot EQ\),若存在,求出点\(Q\)的坐标;若不存在说明理由;
\((3)\)若过\(O\)点作直线\(l\)的平行线交椭圆\(C\)于点\(M\),求\(\dfrac{\left| AD \right|+\left| AE \right|}{\left| OM \right|}\)的最小值.
题型:填空题 题类:其他 难易度:难
年份:2018
\((1)\)已知\(a\in R\),\(i\)为虚数单位,若\(\dfrac{a-i}{2+i}\)为实数,则\(a\)的值为 __.
\((2)\)若直线\(l\)过点\((3,0)\)与双曲线\(4{{x}^{2}}-9{{y}^{2}}=36\)只有一个公共点,则这样的直线有 条
\((3)\)函数\(f(x)=\ln (4+3x-x^{2})\)的单调递减区间是____________
\((4)\)抛物线\({{y}^{2}}=2px\left( p > 0 \right)\)的焦点为\(F\),\(A\),\(B\)为抛物线上的两点,以\(AB\)为直径的圆过点\(F\),过\(AB\)的中点\(M\)作抛物线的准线的垂线\(MN\),垂足为\(N\),则\(\dfrac{\left| MN \right|}{\left| AB \right|}\)的最大值为_____.
题型:选择题 题类:其他 难易度:难
测年份:2018
已知直线\(l\):\((m{+}2)x{+}(m{-}1)y{+}4{-}4m{=}0\)上总存在点\(M\),使得过\(M\)点作的圆\(C\):\(x^{2}{+}y^{2}{+}2x{-}4y{+}3{=}0\)的两条切线互相垂直,则实数\(m\)的取值范围是\(({ })\)