题型:填空题 题类:月考试卷 难易度:难
年份:2018
\((1)\)直线\(y=4x\)与曲线\(y=4x^{3}\)在第一象限内围成的封闭图形的面积为______ .
\((2)\) 一同学在电脑中打出如下图形\((○\)表示空心圆,\(●\)表示实心圆\()○●○○●○○○●○○○○●…\)若将此若干个圆依此规律继续下去,得到一系列的圆,那么前\(2010\)个圆中有实心圆的个数为______ .
\((3)\)若\((x+2+m)^{9}=a_{0}+a_{1}(x+1)+a_{2}(x+1)^{2}+…+a_{9}(x+1)^{9}\)且\((a_{0}+a_{2}+…+a_{8})^{2}-(a_{1}+a_{3}+…+a_{9})^{2}=3^{9}\),则实数\(m\)的值是______ .
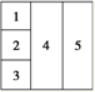
\((4)\) 如图,用\(4\)种不同的颜色对图中\(5\)个区域涂色\((\) \(4\)种颜色全部使用 \()\),要求每个区域涂一种颜色,相邻的区域不能涂相同的颜色,则不同的涂色方法有______ 种\(.(\)用数字作答\()\)
题型:填空题 题类:月考试卷 难易度:难
年份:2018
\((1)\)若\((x+a)(1+2x{)}^{5} \)的展开式中\(x^{3}\)的系数为\(20\),则\(a=\)__________.
\((2)\)一个正方体的各顶点均在同一球的球面上,若该球的体积为\(4\sqrt{3}\pi \),则该正方体的表面积为_________\(.\)
\((3)\)对于三次函数\(f(x)=a{x}^{3}+b{x}^{2}+cx+d(a\neq 0) \),给出定义:设\(f{{'}}(x)\)是函数\(y=f(x)\)的导数,\(f{{'}}{{'}}(x)\)是\(f{{'}}(x)\)的导数,若方程\(f{{'}}{{'}}(x)=0\)有实数解\(x_{0}\),则称点\((x\)\(0\), \(f(x\)\(0\)\())\)为函数的“拐点”\(.\)经过探究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且“拐点”就是对称中心\(.\)设函数\(g(x)=2{x}^{3}-3{x}^{2}+1 \),则\(g( \dfrac{1}{100})+g( \dfrac{2}{100})+……+g( \dfrac{99}{100})= \) ____________.
\((4)\)已知函数\(f(x)=\ln (x+|x|)- \dfrac{1}{1+{x}^{2}} \),命题\(p\):实数\(x\)满足不等式\(f(x+1) > f(2x-1)\);命题\(q\):实数\(x\)满足不等式\({x}^{2}-(m+1)x+m\leqslant 0 \),若\(¬p \)是\(¬q \)的充分不必要条件,则实数\(m\)的取值范围是__________.