题型：解答题 题类：月考试卷 难易度：中档
年份：2018
如图，在三棱柱\(ABC-{{A}_{1}}{{B}_{1}}{{C}_{1}}\)中，侧棱\(A{{A}_{1}}\bot \)底面\(ABC\)，\(AB=AC=2\)，\(\angle BAC=120{}^\circ \)，\(A{{A}_{1}}=3\)，\(D\)，\({{D}_{1}}\)分别是\(BC\)，\({{B}_{1}}{{C}_{1}}\)上的中点，\(P\)是线段\(AD\)上的一点\((\)不包括端点\()\)．
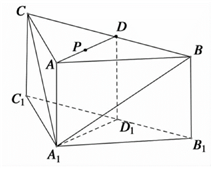
\((1)\)在平面\(ABC\)内，试作出过点\(P\)与平面\({{A}_{1}}BC\)平行的直线\(l\)，并证明直线\(l\bot \)平面\(AD{{D}_{1}}{{A}_{1}}\)；
\((2)\)设\((1)\)中的直线\(l\)交\(AC\)于点\(Q\)，求三棱锥\({{A}_{1}}-Q{{C}_{1}}D\)的体积．
题型：选择题 题类：月考试卷 难易度：中档
测年份：2018
设\(m\)，\(n\)是两条不同的直线，\(\alpha\)，\(\beta\)是两个不同的平面，则正确的结论是\((\) \()\)
题型：填空题 题类：月考试卷 难易度：中档
年份：2018
\(α\)，\(β\)是两个平面，\(m\)，\(n\)是两条直线，有下列四个命题：
\(①\)如果\(m⊥n\)，\(m⊥α\)，\(n/\!/β\)，那么\(α⊥β\)．
\(②\)如果\(m⊥α\)，\(n/\!/α\)，那么\(m⊥n\)．
\(③\)如果\(α/\!/β\)，\(m⊂α\)，那么\(m/\!/β\)．
\(④\)如果\(m/\!/n\)，\(α/\!/β\)，那么\(m\)与\(α\)所成的角和\(n\)与\(β\)所成的角相等．
其中正确的命题有________\(.(\)填写所有正确命题的编号\()\)
一个几何体的平面展开图如右图所示，其中四边形ABCD为正方形，E、F分别为PB、PC的中点，在此几何体中，下面结论中一定正确的是（ ） 
