题型：选择题 题类：期末考试 难易度：中档
测年份：2018
在证明命题：“若空间两条直线\(a,b\)分别垂直于平面\(\alpha \)，则\(a/\!/b.\)”时，学生小夏这样证明：设\(a,b\)与面\(\alpha \)分别相交于\(A,B\)，连接\(A,B\)．
\(\because a\bot \alpha ,b\bot \alpha ,AB\subset \alpha \)，\(①\)
\(\therefore a\bot AB,b\bot AB\)，\(②\)
\(\therefore a/\!/b.③\)
这里的证明有两个推理，
\(p\)：\(①\Rightarrow ②\)，\(q\)：\(②\Rightarrow ③\)，则下列命题为真命题的是
题型：填空题 题类：期末考试 难易度：中档
年份：2018
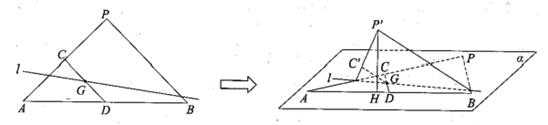
如图，等腰\(\vartriangle PAB\)所在平面为\(\alpha \)，\(PA\bot PB\)，\(AB=4\)，点\(C\)，\(D\)分别为\(PA\)，\(AB\)的中点，点\(G\)为\(CD\)的中点\(.\)平面\(\alpha \)内经过点\(G\)的直线\(l\)将\(\vartriangle PAB\)分成两部分，把点\(P\)所在的部分沿直线\(l\)翻折，使点\(P\)到达点\(P{{{'}}}(P{{{'}}}\notin \)平面\(\alpha ).\)若点\(P{{{'}}}\)在平面\(\alpha \)内的射影\(H\)恰好在翻折前的线段\(AB\)上，则线段\(P{{{'}}}H\)的长度的取值范围是__________．
m的是（ ） 
α，m⊥β，α⊥β
β
α，m
β，α
β
α，m
β，α⊥β
如图，正方体ABCD-A1B1C1D1中，M，N分别是AB，A1D1的中点．判断直线MN与平面BB1D1D的位置关系，并说明理由． 
的正三角形时，求四面体V-DEB的体积． 
