题型:解答题 题类:月考试卷 难易度:较难
年份:2018
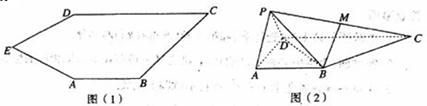
\((1)\)求证:平面\(PAD\bot \)平面\(ABCD\);
\((2)\)若直线\(PC\)与\(AB\)所成角的正切值为\(\dfrac{1}{2}\),求直线\(BM\)与平面\(PDB\)所成角的正弦值.
题型:解答题 题类:月考试卷 难易度:较难
年份:2018
如图,\(P\)是菱形\(ABCD\)所在平面外一点,\(\angle BAD={{60}^{{}^\circ }}\),\(\Delta PCD\)是等边三角形,\(AB=2\),\(PA=2\sqrt{2}\),\(M \)是\(PC\)的中点,点\(G\)为线段\(DM\)上一点\((\)端点除外\()\),平面\(APG\)与\(BD\)交于点\(H\).
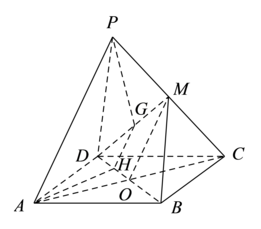
\((1)\)求证:\(PA/\!/GH\);
\((2)\)求证:\(BD\bot \)平面\(PAC\);
\((3)\)求\(AC\)与平面\(BDM\)所成角的正弦值.