4.3.1 直线与平面平行-山东版高教版（拓展上）数学同步练习题

题型：

全部选择题填空题解答题

难易程度：

全部易较易中档较难难

题类筛选：

全部历年真题模拟题期末考试期中考试月考试卷单元测试其他

年份：

全部 2022 2021 2020 2019 2018 2017 更早

总题量：10 选择本页全部试题

题型：解答题题类：其他难易度：较难

年份：2018

如图，已知在直四棱柱\(ABCD-A_{1}B_{1}C_{1}D_{1}\)中，\(AD⊥DC\)，\(AB/\!/DC\)，\(DC=DD_{1}=2AD=2AB=2\)．

\((1)\)求证：\(DB⊥\)平面\(B_{1}BCC_{1}\)；
\((2)\)设\(E\)是\(DC\)上一点，试确定\(E\)的位置，使得\(D_{1}E/\!/\)平面\(A_{1}BD\)，并说明理由．

查看解析收藏纠错相似题

+选题
题型：解答题题类：其他难易度：较难

年份：2018

如图，在直四棱柱\(ABCD-A_{1}B_{1}C_{1}D_{1}\)中，已知\(DC=DD_{1}=2AD=2AB\)，\(AD⊥DC\)，\(AB/\!/DC\)．

\((1)\)求证：\(D_{1}C⊥AC_{1}\)；

\((2)\)问在棱\(CD\)上是否存在点\(E\)，使\(D_{1}E/\!/\)平面\(A_{1}BD.\)若存在，确定点\(E\)位置；若不存在，说明理由．

查看解析收藏纠错相似题

+选题
题型：解答题题类：其他难易度：较难

年份：2018

如图，四棱锥\(P{-}{ABCD}\)中，\({AB}{/\!/}{CD}\)，\({AB}{=}\dfrac{1}{2}{CD}{=}1\)，\(E\)为\({PC}\)中点．

\((1)\)证明：\({BE}{/\!/}\)平面\({PAD}\)；

\((2)\)若\({AB}{⊥}\)平面\({PBC}\)，\({ΔPBC}\)是边长为\(2\)的正三角形，求点\(E\)到平面\({PAD}\)的距离．

查看解析收藏纠错相似题

+选题
题型：解答题题类：其他难易度：较难

年份：2018

\(1\)

如图，四边形\(ABEF\)和四边形\(ABCD\) 均是直角梯形，\(∠FAB=∠DAB=90^{\circ}\)，二面角\(F-AB-D\)是直二面角，\(BE/\!/AF\)，\(BC/\!/AD\)，\(AF=AB=BC=2\)，\(AD=1\)．

\((1)\)证明：在平面\(BCE\)上，一定存在过点\(C\)的直线\(l\)与直线\(DF\)平行；
\((2)\)求二面角\(F-CD-A\)的余弦值．

查看解析收藏纠错相似题

+选题
题型：解答题题类：其他难易度：较难

年份：2018

如图，正方形\(ADEF\)与梯形\(ABCD\)所在的平面互相垂直，\(AB/\!/CD\)，\(AB⊥BC\)，\(DC=BC= \dfrac{1}{2}AB=1\)，点\(M\)在线段\(EC\)上．

\((1)\)证明：平面\(BDM⊥\)平面\(ADEF\)；

\((2)\)若\(AE/\!/\)平面\(MDB\)，求三棱锥\(E-BDM\)的体积．

查看解析收藏纠错相似题

+选题
题型：解答题题类：其他难易度：较难

年份：2018

在如图所示的几何体中，平面\(ACE⊥\)平面\(ABCD\)，四边形\(ABCD\)为平行四边形，\(∠ACB=90^{\circ}\)，\(EF/\!/BC\)，\(AC=BC=\sqrt{{2}}\)，\(AE=EC=1\)．

\((1)\)求证：\(AE⊥\)平面\(BCEF\)；

\((2)\)求\(F\)到平面\(ABCD\)的距离；

\((3)\)求三棱锥\(B-ACF\)的体积．

查看解析收藏纠错相似题

+选题
题型：解答题题类：其他难易度：较难

年份：2018

已知四棱锥\(S-ABCD\)中，底面\(ABCD\)是边长为\(2\)的菱形，\(∠BAD=60^{\circ}\)，\(SA=SD=\sqrt{{5}}\)，\(SB=\sqrt{{7}}\)，点\(E\)是棱\(AD\)的中点，点\(F\)在棱\(SC\)上，且\(\dfrac{SF}{SC}=\lambda \)，\(SA/\!/\)平面\(BEF\)．

\((1)\)求实数\(λ\)的值；

\((2)\)求三棱锥\(F-EBC\)的体积．

查看解析收藏纠错相似题

+选题
题型：解答题题类：其他难易度：较难

年份：2018

如图，在底面是菱形的四棱锥\(P-ABCD\)中，\(PA\bot \)平面\(ABCD\)，\(\angle ABC=60{}^\circ ,PA=AB=2\)，点\(E\)，\(F\)分别为\(BC\)，\(PD\)的中点，设直线\(PC\)与平面\(AEF\)交于点\(Q\)．

\((1)\)已知平面\(PAB\cap \)平面\(PCD=l\)，求证：\(AB/\!/l\)．

\((2)\)求直线\(AQ\)与平面\(PCD\)所成角的正弦值．

查看解析收藏纠错相似题

+选题
题型：解答题题类：其他难易度：较难

年份：2018

如图，四棱锥\(S-ABCD\)中，底面\(ABCD\)是菱形，其对角线的交点为\(O\)，且\(SA=SC,SA\bot BD\)．

\((1)\)求证：\(SO\bot \)平面\(ABCD\)；

\((2)\)设\(\angle BAD=60{}^\circ \)，\(AB=SD=2\)，\(P\)是侧棱\(SD\)上的一点，且\(SB/\!/\)平面\(APC\)，求三棱锥\(A-PCD\)的体积．

查看解析收藏纠错相似题

+选题
题型：解答题题类：其他难易度：较难

年份：2018

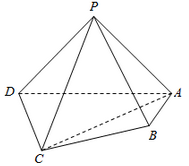
如图，在四棱锥\(P-ABCD\)中，平面\(PAD⊥\)平面\(ABCD\)，\(PA⊥PD\)，\(PA=PD\)，\(AB⊥AD\)，\(AB=1\)，\(AD=2\)，\(AC=CD= \sqrt {5}\)．
\((\)Ⅰ\()\)求证：\(PD⊥\)平面\(PAB\)；
\((\)Ⅱ\()\)求直线\(PB\)与平面\(PCD\)所成角的正弦值；
\((\)Ⅲ\()\)在棱\(PA\)上是否存在点\(M\)，使得\(BM/\!/\)平面\(PCD\)？若存在，求\( \dfrac {AM}{AP}\)的值，若不存在，说明理由．

查看解析收藏纠错相似题

+选题

高中

选择章节

服务介绍

帮助中心