题型:解答题 题类:期末考试 难易度:较难
年份:2018

题型:解答题 题类:期末考试 难易度:较难
年份:2018
如图,三棱柱\(ABC-{{A}_{1}}{{B}_{1}}{{C}_{1}}\)中,\(AB\bot \)平面\(A{{A}_{1}}{{C}_{1}}C\),\(A{{A}_{1}}=AB=AC=2\),\(\angle {{A}_{1}}AC={{60}^{{}^\circ }}\).过\(A{{A}_{1}}\)的平面交\({{B}_{1}}{{C}_{1}}\)于点\(E\),交\(BC\)于点\(F\).
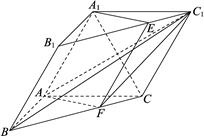
\((\)Ⅰ\()\)求证:\({{A}_{1}}C\bot \)平面\(AB{{C}_{1}}\);
\((\)Ⅱ\()\)求证:四边形\(A{{A}_{1}}EF\)为平行四边形;
\((\)Ⅲ\()\)若\(\dfrac{BF}{BC}=\dfrac{2}{3}\),求二面角\(B-A{{C}_{1}}-F\)的大小.