题型：选择题 题类：期末考试 难易度：较易
新 测年份：2021
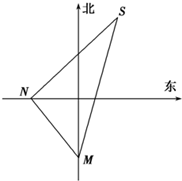如图，一货轮航行到\(M\)处，测得灯塔\(S\)在货轮的北偏东\(15°\)，与灯塔\(S\)相距\(20\)海里，随后货轮按北偏西\(30°\)的方向航行\(30\)分钟到达\(N\)处后，又测得灯塔在货轮的东北方向，则货轮的速度为\((\quad)\) 题型：选择题 题类：期末考试 难易度：较易
新 测年份：2021
题型：选择题 题类：期末考试 难易度：较易
新 测年份：2021
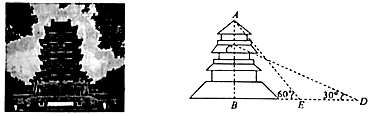
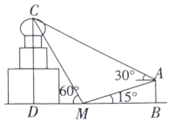某宝塔主体是由圆柱、棱柱、球等几何体构成，如图所示．为了测量宝塔的高度\(CD\)，某数学兴趣小组在宝塔附近选择楼房\(AB\)作为参照物，楼房高为\(10(\sqrt{3}-1)m\)，在楼顶\(A\)处测得地面点\(M\)处的俯角为\(15°\)，宝塔顶端\(C\)处的仰角为\(30°\)，在\(M\)处测得宝塔顶端\(C\)处的仰角为\(60°\)，其中\(B\)，\(M\)，\(D\)在一条直线上，则该宝塔的高度\(CD=(\quad)\) 题型：选择题 题类：期末考试 难易度：较易
新 测年份：2021
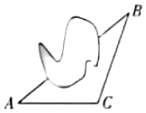如图所示，为了测量某湖泊两侧\(A\)，\(B\)间的距离，甲同学首先选定了与\(A\)，\(B\)不共线的一点\(C(\triangle ABC\)的内角\(A\)，\(B\)，\(C\)所对的边分别记为\(a\)，\(b\)，\(c)\)，然后给出了\(4\)种测量方案：①测量\(A\)，\(C\)，\(b\)；②测量\(a\)，\(b\)，\(C\)；③测量\(A\)，\(B\)，\(a\)；④测量\(A\)，\(b.\)则一定能确定\(A\)，\(B\)间的距离的所有方案的序号为\((\quad)\) 
某市需拍卖一块近似圆形的土地\((\)如图\()\)，内接于圆的平面四边形\(ABCD\)作为建筑用地，周边需做绿化．因地面限制，只能测量出\(AB=1km\)，\(AD=2km\)，测角仪测得\(∠BAD=120°.\)
如图，要测量河对岸的塔高\(AB.\)请设计一个方案，包括：
如图所示，为测量山高\(MN\)，选择\(A\)和另一座山的山顶\(C\)为测量观测点．从\(A\)点测得\(M\)点的仰角\(∠MAN=60°\)，\(C\)点的仰角\(∠CAB=45°\)以及\(∠MAC=75°\)；从\(C\)点测得\(∠MCA=60°.\)已知山高\(BC=500m\)，则山高\(MN=\)______\(m.\) 
数学兴趣小组为了测量电视塔\(AB\)的高度，在塔底水平面上设置两个观测点\(C\)，\(D\)，\(CD\)间距离为\(108\)米，在点\(C\)处测得\(A\)，\(D\)的张角为\(60°\)，在点\(D\)处测得\(A\)，\(C\)的张角为\(75°\)，测得点\(B\)的仰角为\(60°\)，则塔高\(AB=\)______米． 