题型：解答题 题类：期末考试 难易度：较易
新年份：2021
设数列\(\left\{\begin{array}{l}a_{n}\end{array}\right\}\)的前\(n\)项和为\(S_{n}\)，已知\(a_{1}=4\)，\(S_{n}=a_{n+1}+2n-4\)，\(n\in N^{*}.\)
\((1)\)求数列\(\left\{\begin{array}{l}a_{n}\end{array}\right\}\)的通项公式；
\((2)\)设\(b_{n}=\dfrac{a_{n}-2}{\left({2^{n}+1}\right)\left({2^{n+1}+1}\right)}\)，数列\(\left\{\begin{array}{l}b_{n}\end{array}\right\}\)的前\(n\)项和为\(T_{n}\)，求满足\(T_{n}>\dfrac{13}{40}\)的正整数\(n\)的最小值．
题型：解答题 题类：期末考试 难易度：较易
新年份：2021
如图，已知动圆\(M\)过点\(E\left({-1,0}\right))\)，且与圆\(F:\left({x-1}\right)^{2}+y^{2}=8\)内切，设动圆圆心\(M\)的轨迹为曲线\(C.\)
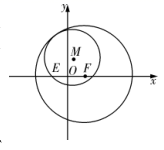
\((1)\)求曲线\(C\)的方程；
\((2)\)过圆心\(F\)的直线\(l\)交曲线\(C\)于\(A\)，\(B\)两点，问：在\(x\)轴上是否存在定点\(P\)，使当直线\(l\)绕点\(F\)任意转动时，\(\overrightarrow {PA}⋅\overrightarrow {PB}\)为定值？若存在，求出点\(P\)的坐标和\(\overrightarrow {PA}⋅\overrightarrow {PB}\)的值；若不存在，请说明理由．
题型：解答题 题类：期末考试 难易度：较易
新年份：2021
题型：解答题 题类：期末考试 难易度：较易
新年份：2021
如图，在三棱锥\(O-ABC\)中，\(OA=1\)，\(OB=2\)，\(OC=3\)，且\(OA\)，\(OB\)，\(OC\)两两夹角都为\(θ.\)